Vectorized computation of basis functions gradients¶

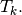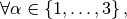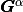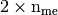By construction, the gradients of basis functions are constants on each element $T_k.$ So, we denote, $\forall \il\in\ENS{1}{3},$ by $\vecb{G}^\il$ the $2 \times \nme$ array defined, 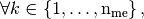$\forall k\in\ENS{1}{\nme},$ by

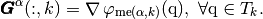
$\vecb{G}^\il(:,k)= \GRAD\BasisFunc_{\me(\il,k)}(\q),\ \forall \q\in T_k.$

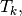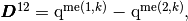
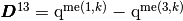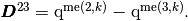On a triangle $T_k,$ we denote by $\vecb{D}^{12}=\q^{\me(1,k)}-\q^{\me(2,k)},$ $\vecb{D}^{13}=\q^{\me(1,k)}-\q^{\me(3,k)}$ and $\vecb{D}^{23}=\q^{\me(2,k)}-\q^{\me(3,k)}.$ Then, we have

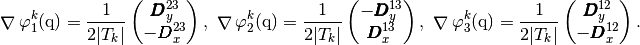
$\GRAD\BasisFunc_{1}^k(\q)=\frac{1}{2|T_k|} \begin{pmatrix} \vecb{D}^{23}_y\\-\vecb{D}^{23}_x \end{pmatrix},\ \GRAD\BasisFunc_{2}^k(\q)=\frac{1}{2|T_k|} \begin{pmatrix} -\vecb{D}^{13}_y\\\vecb{D}^{13}_x \end{pmatrix},\ \GRAD\BasisFunc_{3}^k(\q)=\frac{1}{2|T_k|} \begin{pmatrix} \vecb{D}^{12}_y\\-\vecb{D}^{12}_x \end{pmatrix}.$

With these formulas, we obtain the vectorized algorithm given in Algorithm 134.

Algorithm 134

Figure 134: Vectorized algorithm for computation of basis functions gradients in 2d

Navigation

Vectorized computation of basis functions gradients¶

This Page

Quick search

Navigation