Quelques expérimentations avec un métronome trouvé en vide-grenier
Il y a quelques mois j'ai trouvé un métronome mécanique d'occasion à 3€ en vide grenier, que j'ai acheté pour remplacer mon appli métronome
par quelque chose avec un peu plus de style.

Je commence à l'utiliser, mais j'ai la vague impression qu'il est très légèrement irrégulier ; ça arrive facilement, dès qu'un métronome n'est pas
posé parfaitement à plat, il se met à swinguer car l'oscillation du pendule devient asymétrique. Et puis, il est peut-être un peu vieux ou mal calibré. C'était probablement le cas, mais je me suis
dit que l'enregistrer et regarder l'onde sur audacity confirmerait mes doutes. Je remarque que le "tic" est effectivement plus court que le "tac" (il y a un petit swing), mais que les rapports de durée s'inversent après quelques pulsations...
Intrigué, je décide donc avec un petit script python de faire un graphe du taux de swing en fonction du temps, c'est à dire "durée du tic"/"durée d'un tic+tac".

On observe clairement un motif périodique dans l'évolution du taux de swing (??). J'essaye avec plusieurs choix de tempo différents sur le métronome, mais j'observe que la période du motif ne dépend que
du nombre de battements et pas du tempo. La période de l'oscillation est toujours d'exactement 18 battements.
Plus bizarre encore, j'observe la même 18-périodicité non pas sur le taux de swing, mais sur le tempo lui-même. Mais il y a aussi une oscillation de période beaucoup plus grande (environ 200 battements). Voilà le graphe du tempo moyen sur un aller retour (tic+tac) en bpm en fonction du nombre de battements écoulés:
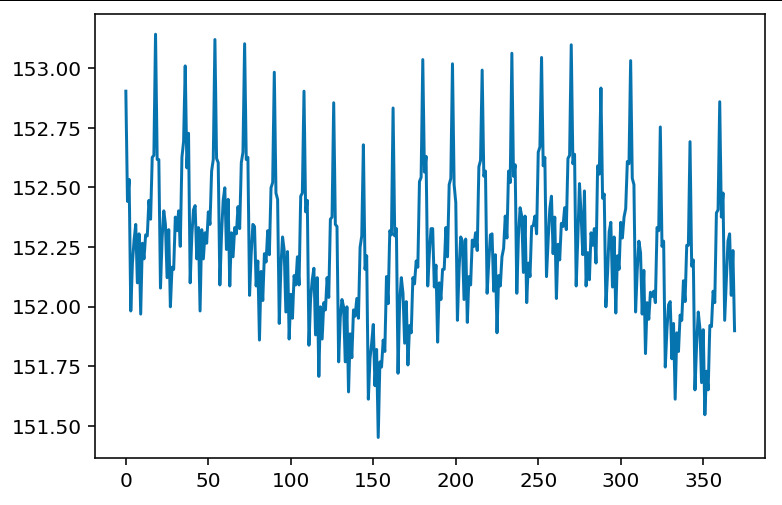
Si j'enregistre le tempo sur plusieurs minutes, il exhibe une variation d'un troisième ordre : il augmente petit à petit (environ 1bpm tous les 1000 battements).
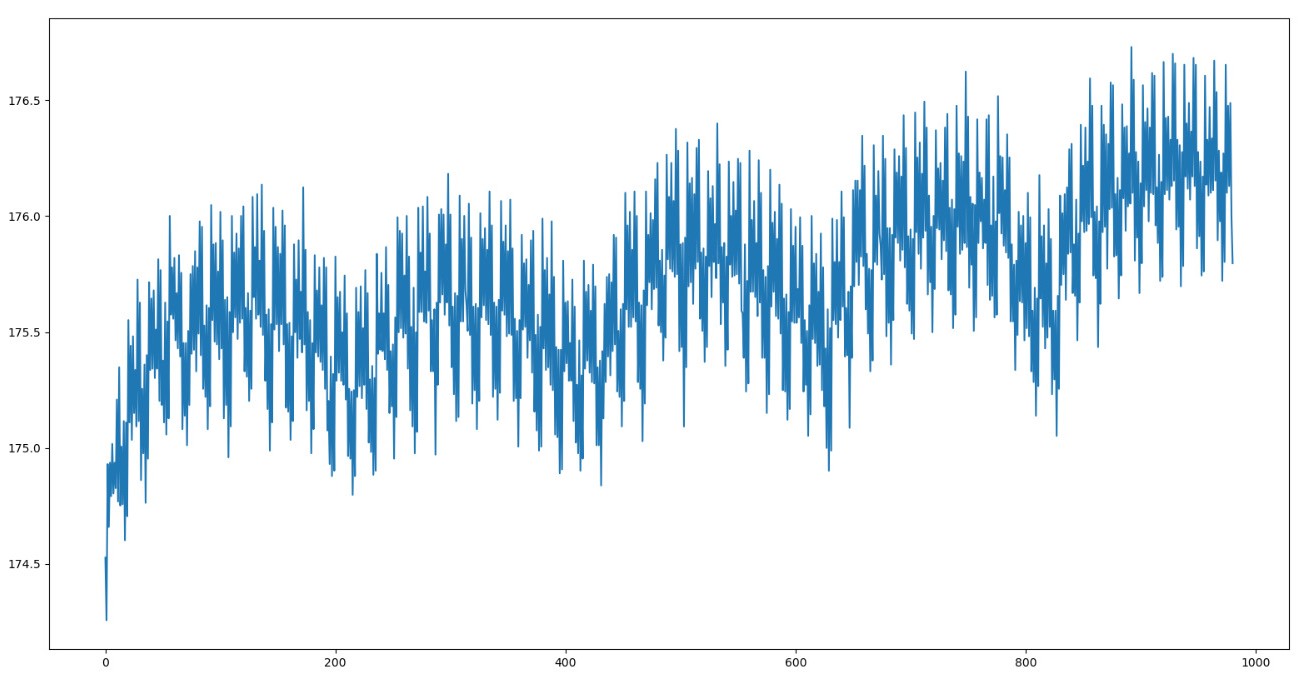
Le truc vraiment surprenant est que l'oscillation lente (période 200) n'est absolument pas présente sur le swing, mais uniquement sur le tempo. Observons le spectre des fourier de mes deux signaux (taux de swing et tempo en fonction du temps):
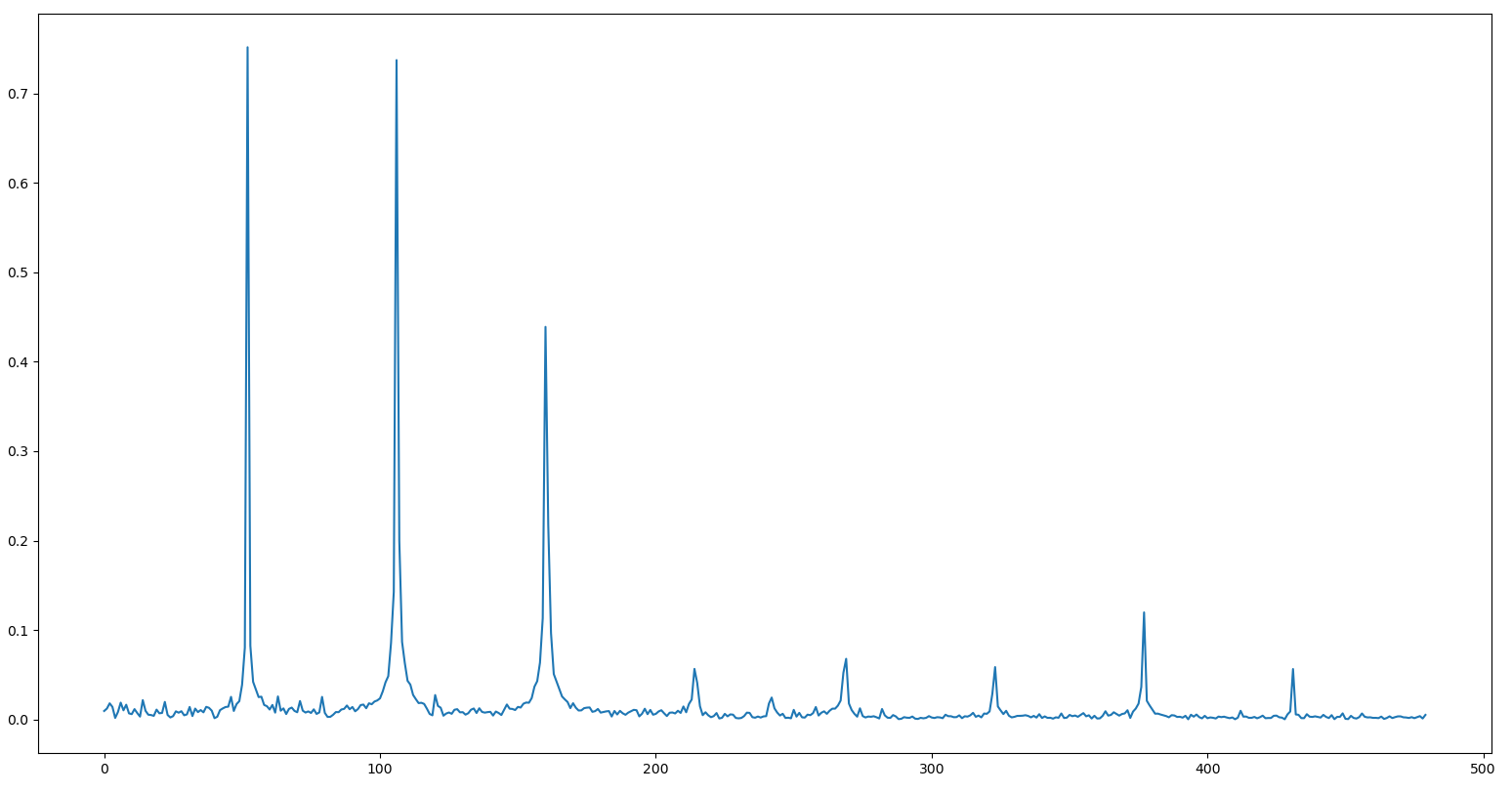
Spectre du taux de swing :
Spectre du tempo :
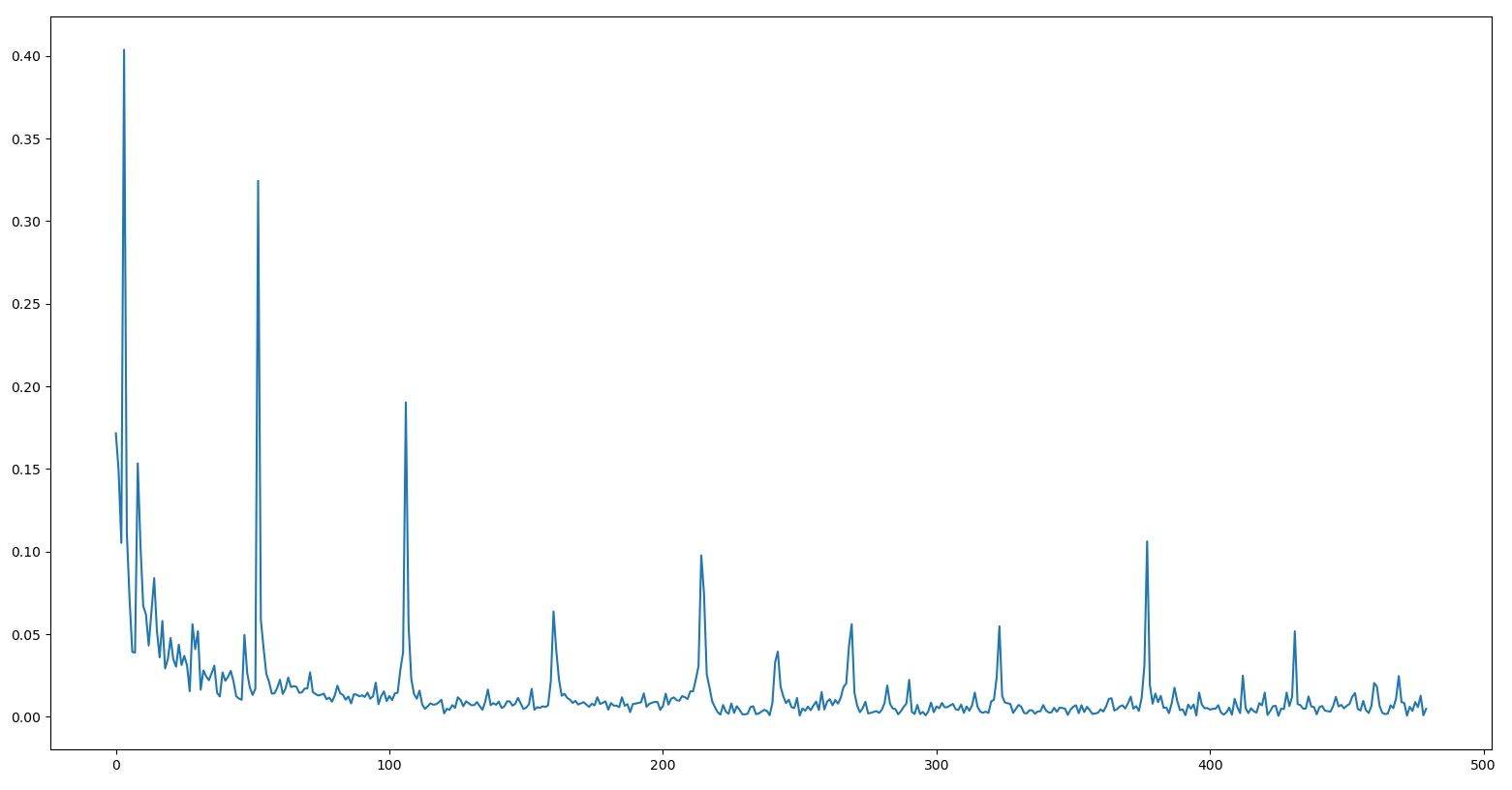
L'échelle en abcisse ne veut rien dire, mais dites vous que le premier pic dans le taux de swing correspond à une fréquence de $(18)^{-1} b^{-1}$ (battements$^{-1}$).
Deux choses sont frappantes dans ces graphes : la 18-périodicité est très très nette sur le taux de swing, et on observe même quelques harmoniques, dont les plus nets sont clairement les 2e et 3e.
La deuxième chose étonnante est qu'on voit bien le pic en très basse fréquence pour le tempo ($200^{-1} b^{-1}$) qui n'apparaît absolument pas dans le spectre du swing.
Visiblement, il y a un mécanisme qui engendre une irrégularité de période 18 à l'intérieur du métronome. Peut-être un engrenage à 18 dents qui est mal usiné ? Après avoir passé (beaucoup trop de) temps sur la page wikipédia des mécanismes à échappement, je décide de démonter la bête pour en avoir le coeur net :

Parmi les engrenages, le dernier (celui qui alimente le mécanisme d'échappement en bout de chaîne) ressemble à ça :


18 dents exactement ! J'imagine qu'il a quelques irrégularités de fabrications qui engendrent les soucis de swing du métronome. Ce qui reste mystérieux c'est le volume des 3 pics dans le spectre et pourquoi les harmoniques suivantes sont si faibles.
Si quelqu'un a un modèle pour expliquer ça, ça m'intéresse.
Ca ne résoud cependant pas le deuxième mystère de l'oscillation de basse fréquence, de période $200$. Mais je remarque lors de l'enregistrement qu'il y a exactement 5 oscillations de ce genre (sur 1000 battements) alors que la molette qui recharge le ressort interne fait exactement 5 tours...
Je suppose que le ressort n'est pas entièrement régulier dans la force qu'il fournit au mécanisme en fonction de son orientation, ou bien que l'engrenage qu'il enclenche (j'avoue que j'ai eu la flemme de compter les dents : mais il y en a beaucoup.) comporte ~= 200 dents et a aussi des irrégularités.
En tout cas c'était 3€ bien rentabilisés.









