M.A.C.S.

MACS3, ANALYSE NUMERIQUE AVANCEE :

METHODES DE DECOMPOSITION DE DOMAINES

Volume: 39h

Enseignants: L. Halpern (PU, LAGA, Paris 13), J. Ryan (Ingénieur ONERA Calcul haute performance)

Contrôle des connaissances : Examen + Projet encadré

UE : Matières de base

Motivation du cours : Des phénomènes physiques de plus en plus complexes sont modélisés par des systèmes d'équations aux dérivées partielles. Ces équations sont elles-mêmes discrétisées pour être résolues par ordinateur. Si les progrès technologiques ont constamment amélioré les performances des processeurs, ces performances atteignent aujourd'hui un plateau en terme de mémoire et de puissance de calcul. Les ordinateurs monoprocesseurs ont laissé la place aux quadricœurs pour les ordinateurs de bureau, aux ordinateurs parallèles à mémoire distribuée pour les calculs actuels qui nécessitent de calculer en parallèle sur un grand nombre de processeurs (le plus gros ordinateur actuel est un FUJITSU formé de 548 352 processeurs, qui développe une puissance de calcul de 10 petaflops). Pour utiliser au mieux ces calculateurs parallèles formés d'un grand nombre de processeurs, il fallait inventer de nouveaux algorithmes parallèles. Les méthodes de décomposition de domaine sont naturellement adaptées à cette problématique, pour des systèmes complexes issus de la modélisation. Elles permettent de structurer et gérer le domaine géométrique en sous-domaines. Pour chaque sous-domaine, les données du problème (géométrie, coefficients) et les calculs sont dédiés à un nœud du multiprocesseur, et la communication entre les nœuds reproduit divers types de transmission entre les sous-domaines.

Objectifs du cours : Ce cours se propose de donner un aperçu des diverses méthodes de décomposition de domaines, inventées au fil du temps dans divers contextes. Pour guider l'étudiant, nous donnerons un problème modèle simple sur lequel nous introduirons les principaux concepts et mécanismes, chaque fois illustrés par des petits programmes Matlab qu’il pourra faire tourner pour comprendre.

Prérequis : Cours MACS 1 et 2, ou M1 de mathématiques.

Documents

Document du cours

Poly MACS 1 sur les systèmes linéaires. Chapitre de rappels.

Les codes du TP.

Contenu du cours :

1) Rappels sur les méthodes itératives de résolution de systèmes linéaires (Jacobi, Gauss-Seidel,SOR, gradient)

2) Méthodes de Schwarz

a) Méthodes alternée et parallèle.

b) Méthodes de Schwarz discrètes.

c) Méthodes de Schwarz et préconditionnement

3) Méthode de Schur

a) Schur primal

b) Schur dual

c) Feti et Neumann-Neumann

d) Dirichlet-Neumann et Neumann-Dirichlet.

4) Préconditionneur grille grossière.

D’autre part trois séances seront consacrées à la réalisation d’un projet de décomposition de domaines.

Ce projet consistera en l’application et comparaison de ces méthodes à la résolution des équations d’Euler linéarisé instationnaire par un schéma temporel implicite. Un code explicite 2D sera fourni.

La note de ce projet constituera la moitié de la note du cours.

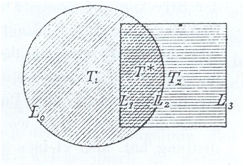
                     Exemples de décomposition de domaines