OptFEM2DP1 Toolbox  V1.2b3
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 2D
 All Files Functions Pages
OptFEM2DP1

Introduction

OptFEM2DP1 is a MATLAB©/GNU Octave© library providing simple and efficient vectorized routines for 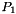$ P_1 $-Lagrange Finite Element Methods in 2D

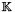  • Version 1.2 : We add the assembly of the Stiffness Elasticity Matrix $ \StiffElas $ defined by

    \[ \StiffElas_{m,l}=\int_{\DOMH} \Odv^t(\BasisFuncTwoD_m) \Ocv(\BasisFuncTwoD_l)dT, \ \forall (m,l)\in\ENS{1}{2\,\nq}^2,\]

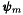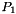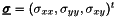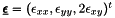    where $ \BasisFuncTwoD_m $ are $ P_1 $-Lagrange vector basis functions. Here $ \Ocv=(\Occ_{xx},\Occ_{yy},\Occ_{xy})^t $ and $ \Odv=(\Odc_{xx},\Odc_{yy},2\Odc_{xy})^t $ are the elastic stress and strain tensors respectively.
  • Version 1.1 : Contains different optimization techniques to perform the assembly of P1 finite element matrices in Matlab and Octave, from the standard approach (basic version and OptV0) to recent vectorized ones (OptV1 and OptV2), without any low level language used. The more efficient version (OptV2) is entirely vectorized (without loop) and without any quadrature formula. We have implemented :
    • the Mass Matrix $ \Masse $ given by

      \[ \Masse_{i,j}=\int_\DOMH \FoncBase_i(\q)\, \FoncBase_j(\q)\, d\q,\ \forall (i,j)\in{\ENS{1}{\nq}}^2 \]

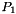      where $ \FoncBase_i $ are $ P_1 $-Lagrange basis functions.
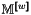    • the Weighted Mass Matrix $ \MasseF{w} $ given by

      \[ \MasseF{w}_{i,j}=\int_\DOMH w(\q)\FoncBase_i(\q) \FoncBase_j(\q) d\q,\ \forall (i,j)\in\ENS{1}{\nq}^2 \]

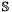    • the Stiffness Matrix $ \Stiff $ given by

      \[ \Stiff_{i,j}=\int_\DOMH \DOT{\GRAD\FoncBase_i(\q)}{\GRAD\FoncBase_j(\q)}d\q,\ \forall (i,j)\in{\ENS{1}{\nq}}^2\]

Quick testing

To test the OptFEM2DP1 library, you can run validation tests (see runValids), in OptFEM2DP1 directory, 

runValids()

or some benchmarks (see runBenchs) 

runBenchs()

Requirements

  • Needs Matlab or GNU Octave 3.6.*

GNU Octave 3.6.3 under linux

GNU Octave 3.6.3 source for Linux is available here.

For a description of our compilation/installation under Ubuntu 12.04 LTS (x86_64) refer to F. Cuvelier homepage, section Octave in left menu.

With GNU Octave 3.6.3, you need to install the following packages: splines, mesh, general. These packages can be found here.

To install a package, please run Octave as root and download the package archive and run 

pkg install package_file_name.tar.gz

GNU Octave 3.6.2 for Windows Microsoft Visual Studio

GNU Octave 3.6.2 is available here.

  • Download file octave-3.6.2-vs2010-setup.exe
  • run it and select, at least, packages splines, mesh and general.

Testing and Working

  • Ubuntu 12.04 LTS (x86_64) with
    • Matlab R2012b
    • Matlab R2012a
    • Matlab R2011b
    • Matlab R2011a
    • GNU Octave 3.6.3
  • Works on Windows 7 64 bits with
    • Matlab R2012b
    • Matlab R2012a
    • GNU Octave 3.6.2

License issues

OptFEM2DP1 is published under the terms of the GNU General Public License.

OptFEM2DP1 is free software: you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation, either version 3 of the License, or (at your option) any later version.

OptFEM2DP1 is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You should have received a copy of the GNU General Public License along with this program. If not, see http://www.gnu.org/licenses/.

Software using source files of this project or significant parts of it, should include the following attribution notice:

% --------------------------------------------------------------------
% ATTRIBUTION NOTICE:
% This product includes software developed for the OptFEM2DP1 project at
% (C) University Paris XIII, Galilee Institute, LAGA, France.
%
% OptFEM2DP1 is a MATLAB/Octave software package for P1-Lagrange Finite Element Methods in 2D.
% The project is maintained by
% F. Cuvelier, C. Japhet and G. Scarella.
% For Online Documentation and Download we refer to
% <www.math.univ-paris13.fr/~cuvelier>
% --------------------------------------------------------------------