 |
OptFEM2DP1 Toolbox
V1.2b3
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 2D
|
 |
OptFEM2DP1 Toolbox
V1.2b3
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 2D
|
Assembly of the Weighted Mass Matrix by 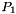 -Lagrange finite elements.
More...
-Lagrange finite elements.
More...
Go to the source code of this file.
Functions | |
| function M = | MassWAssemblingP1base (nq, nme, me, areas, Tw) |
Assembly of the Weighted Mass Matrix by 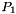 -Lagrange finite elements. -Lagrange finite elements. | |
Assembly of the Weighted Mass Matrix by 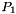 -Lagrange finite elements.
-Lagrange finite elements.
Definition in file MassWAssemblingP1base.m.
| function M = MassWAssemblingP1base | ( | nq, | |
| nme, | |||
| me, | |||
| areas, | |||
| Tw | |||
| ) |
Assembly of the Weighted Mass Matrix by 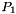 -Lagrange finite elements.
-Lagrange finite elements.
The Weighted Mass Matrix 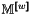 is given by
is given by
![\[\MasseF{w}_{i,j}=\int_\DOMH w(\q)\FoncBase_i(\q) \FoncBase_j(\q) d\q,\ \forall (i,j)\in{\ENS{1}{\nq}}^2\]](form_54.png)
where 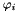 are
are 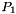 -Lagrange basis functions.
-Lagrange basis functions.
Th=SquareMesh(10);
w=@(x,y) cos(x+y);
Tw=w(Th.q(1,:),Th.q(2,:));
Mw=MassWAssemblingP1base(Th.nq,Th.nme,Th.me,Th.areas,Tw);| nq | total number of nodes of the mesh, also denoted by 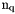 , , |
| nme | total number of triangles, also denoted by 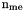 , , |
| me | Connectivity array, 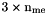 array. array.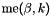 is the storage index of the is the storage index of the 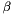 -th vertex of the -th vertex of the 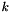 -th triangle in the array -th triangle in the array 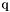 , , 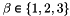 and and 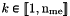 . . |
| areas | Array of areas, 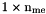 array. areas(k) is the area of the array. areas(k) is the area of the 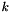 -th triangle. -th triangle. |
| Tw | Array of vertices weight 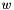 function values, function values, 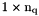 array. array.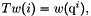 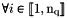 . . |
| M | Global weighted mass matrix, 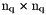 sparse matrix. sparse matrix. |
Definition at line 17 of file MassWAssemblingP1base.m.