 |
OptFEM3DP1 Toolbox
V1.0
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 3D
|
 |
OptFEM3DP1 Toolbox
V1.0
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 3D
|
Compute, for each tetraedra, the gradients of the 4 local 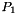 -Lagrange basis functions multiply by
-Lagrange basis functions multiply by 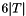 .
More...
.
More...
Go to the source code of this file.
Functions | |
| function G = | ComputeGradientVec (q, me) |
Compute, for each tetraedra, the gradients of the 4 local 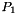 -Lagrange basis functions multiply by -Lagrange basis functions multiply by 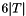 . . | |
Compute, for each tetraedra, the gradients of the 4 local 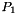 -Lagrange basis functions multiply by
-Lagrange basis functions multiply by 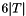 .
.
Definition in file ComputeGradientVec.m.
| function G = ComputeGradientVec | ( | q, | |
| me | |||
| ) |
Compute, for each tetraedra, the gradients of the 4 local 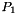 -Lagrange basis functions multiply by
-Lagrange basis functions multiply by 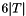 .
.
| q | Array of vertices coordinates, 3-by-nq array. q(il,j) is the il-th coordinate of the j-th vertex, il in {1,3} and j in {1,...,nq}. |
| me | Connectivity array, 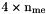 array. array. 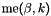 is the storage index of the is the storage index of the 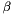 -th vertex of the -th vertex of the 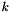 -th tetrahedron in the array -th tetrahedron in the array 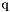 of vertices coordinates, of vertices coordinates, 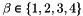 and and 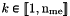 . . |
| G | array of 4 cells. each cell is an 3-by-nme array. |
| G{il}(,k) | is 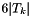 times the gradient of the local times the gradient of the local 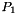 -Lagrange basis function associated to point -Lagrange basis function associated to point 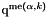 on the the tetrahedron on the the tetrahedron 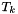 . . |
| Copyright | See License issues |
Definition at line 17 of file ComputeGradientVec.m.