Initialization of a minimalist 3D Mesh structure for the cube domain. More...

Functions
function Th =	CubeMesh (N)
	Initialization of a minimalist 3D Mesh structure for the cube domain.

Detailed Description

Initialization of a minimalist 3D Mesh structure for the cube domain.

Definition in file CubeMesh.m.

Function Documentation

function Th = CubeMesh ( N )

Initialization of a minimalist 3D Mesh structure for the cube domain.

Cube domain is $[0,1]\times[0,1]\times[0,1]$

figure : CubeMesh function with N=3

There are 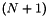$(N+1)$ vertices on each edges and 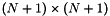$(N+1)\times(N+1)$ vertices on each boundary faces.

Parameters

N	integer, number, minus one, of vertices on a edge

Return values

Th	minimalist mesh structure

Generated fields of Mesh:

nq — total number of vertices, also denoted by 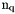$\nq$ .
q — Array of vertices coordinates, 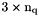$3\times\nq$ array.
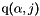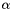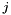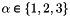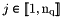
${\q}(\il,j)$ is the $\il$ -th coordinate of the -th vertex, $\il\in\{1,2,3\}$ and $j\in\ENS{1}{\nq}$
nme — total number of elements, also denoted by 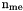$\nme$ .
me — Connectivity array, 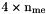$4\times\nme$ array.
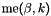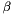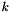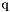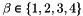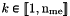$\me(\jl,k)$ is the storage index of the $\jl$ -th vertex of the -th tetrahedron in the array $\q$ of vertices coordinates, $\jl\in\{1,2,3,4\}$ and $k\in{\ENS{1}{\nme}}$ .
volumes — Array of volumes, 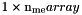$1\times\nme array$ . volumes(k) is the volume of the k-th tetrahedron.

Definition at line 17 of file CubeMesh.m.