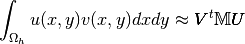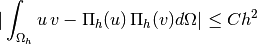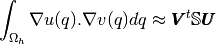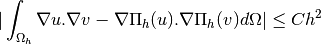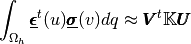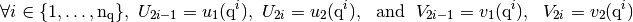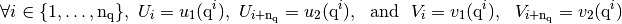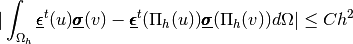valid2D module¶

Contents

Mass Matrix
Stiffness matrix
Elastic Stiffness Matrix

Mass Matrix ¶

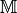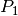Validation program for the assembly of the Mass matrix $\MAT{M}$ for $P_1$ -Lagrange finite element method in 2d (see Mass Matrix).

Test 1: Computation of the Mass Matrix using the base, OptV1 and OptV2 versions : it gives errors and computation times

Test 2: Computation of the integral

$\int_{\Omega_h} u(x,y) v(x,y) dxdy \approx \pmb{V}^t\mathbb{M} \pmb{U}$

where $\pmb{U}_i=u(q^i)$ and $\pmb{V}_i=v(q^i)$ . Functions $u$ and $v$ are those defined in ...

Test 3: Ones retrieves the order 2 of $P_1$ -Lagrange integration

$|\int_{\Omega_h} u\,v -\Pi_h(u)\,\Pi_h(v)d\Omega| \leq C h^2$

Note

source code

pyOptFEM.valid2D.validMass2DP1.validMass2DP1(**kwargs)[source]¶: Validation of Mass Matrix for P1-Lagrange finite elements in 2D

>>> from pyOptFEM.valid2D import validMass2DP1
>>> validMass2DP1()
******************************************
*     Mass Assembling P1 validations     *
******************************************
-----------------------------------------
Test 1: Matrices errors and CPU times
-----------------------------------------
    Matrix size           : (121,121)
    Error P1base vs OptV1 : 8.673617e-19
    Error P1base vs OptV2 : 8.673617e-19
    CPU times base (ref)  : 0.2638 (s)
    CPU times OptV1       : 0.0259 (s) - Speed Up X10.179
    CPU times OptV2       : 0.0016 (s) - Speed Up X160.286
----------------------------
  Test 1 (results): OK
----------------------------
-----------------------------------------------------
  Test 2: Validations by integration on [0,1]x[0,1]
-----------------------------------------------------
    function 0 : u(x,y)=x+2*y, v(x,y)=3*x+y+1,
            -> Mass error=0.000000e+00
    function 1 : u(x,y)=x**2+2*y*x+y, v(x,y)=3*x*y+y**2+1,
            -> Mass error=5.736389e-03
    function 2 : u(x,y)=x**3+2*y**2*x+y**2+x, v(x,y)=2*x*y+y**3+x*y,
            -> Mass error=1.141472e-02
----------------------------
  Test 2 (results): OK
----------------------------
--------------------------------
  Test 3: Validations by order
--------------------------------
  functions 2: u(x,y)=x**3+2*y**2*x+y**2+x, v(x,y)=2*x*y+y**3+x*y
      Matrix size                     : (121,121)
      MassAssemblingP1OptV2 CPU times : 0.001(s)
      Error                           : 1.141472e-02
      Matrix size                     : (441,441)
      MassAssemblingP1OptV2 CPU times : 0.002(s)
      Error                           : 2.825605e-03
      ...
      Matrix size                     : (10201,10201)
      MassAssemblingP1OptV2 CPU times : 0.019(s)
      Error                           : 1.125457e-04

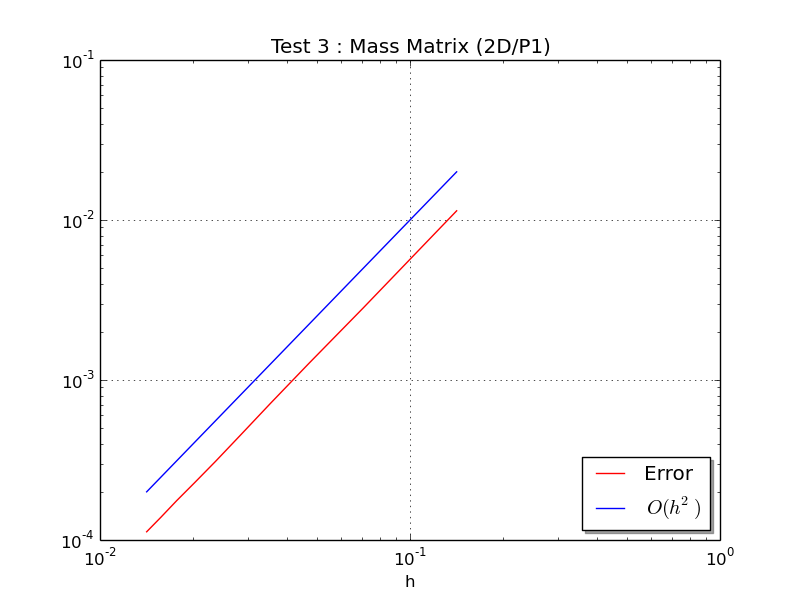
At last, this program plots the figure :

Figure 56: Graphical results of validMass2DP1-Test 3

Stiffness matrix ¶

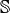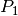Validation function for the assembly of the Stiffness matrix, $\MAT{S}$ , for $P_1$ -Lagrange finite element method in 2d (see Stiffness Matrix)

Test 1: Computation of the Stiffness Matrix using the base, OptV1 and OptV2 versions : it gives errors and computation times

Test 2: Computation of the integral

$\int_{\Omega_h} \nabla u(q).\nabla v(q)dq \approx \pmb{V}^t\mathbb{S} \pmb{U}$

where $\pmb{U}_i=u(q^i)$ and $\pmb{V}_i=v(q^i)$ . Functions $u$ and $v$ are those defined in ...

Test 3: Ones retrieves the order 2 of $P_1$ -Lagrange integration

$|\int_{\Omega_h} \nabla u . \nabla v -\nabla\Pi_h(u) . \nabla\Pi_h(v)d\Omega| \leq C h^2$

Note

source code

pyOptFEM.valid2D.validStiff2DP1.validStiff2DP1(**kwargs)[source]: validation of stiffness matrix assembling functions

>>> from pyOptFEM.valid2D import validStiff2DP1
>>> validStiff2DP1()
**********************************************
*     2D Stiff Assembling P1 validations     *
**********************************************
-----------------------------------------
  Test 1: Matrices errors and CPU times
-----------------------------------------
    Matrix size           : (121,121)
    Error P1base vs OptV1 : 8.881784e-16
    Error P1base vs OptV2 : 4.440892e-16
    CPU times base (ref)  : 0.1519 (s)
    CPU times OptV1       : 0.0106 (s) - Speed Up X14.270
    CPU times OptV2       : 0.0009 (s) - Speed Up X174.238
----------------------------
  Test 1 (results): OK
----------------------------
-----------------------------------------------------
  Test 2: Validations by integration on [0,1]x[0,1]
-----------------------------------------------------
    function 0 : u(x,y)=x+2*y, v(x,y)=3*x+y+1,
          -> Stiff error=2.486900e-14
    function 1 : u(x,y)=x**2+2*y*x+y, v(x,y)=3*x*y+y**2+1,
          -> Stiff error=2.000000e-02
    function 2 : u(x,y)=x**3+2*y**2*x+y**2+x, v(x,y)=2*x*y+y**3+x*y,
          -> Stiff error=1.500000e-02
----------------------------
  Test 2 (results): OK
----------------------------
--------------------------------
  Test 3: Validations by order
--------------------------------
Test 2: u(x,y)=x**3+2*y**2*x+y**2+x, v(x,y)=2*x*y+y**3+x*y
      Matrix size                      : (121,121)
      StiffAssemblingP1OptV2 CPU times : 0.001(s)
      Error                            : 1.500000e-02
      ...
      Matrix size                      : (10201,10201)
      StiffAssemblingP1OptV2 CPU times : 0.021(s)
      Error                            : 1.500000e-04

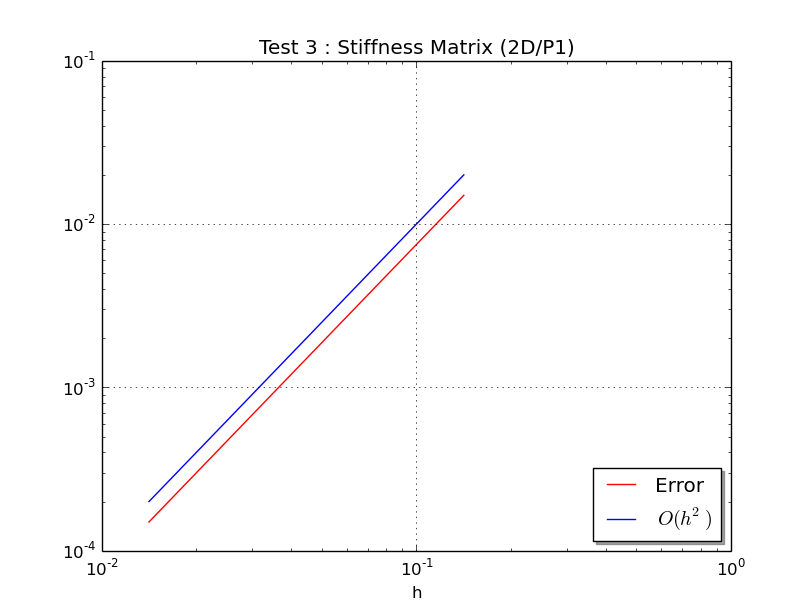
At last, this program plots this figure :

Figure 57: Graphical results of validStiff2DP1-Test 3

Elastic Stiffness Matrix ¶

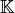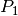Validation function for the assembly of the Elastic Stiffness matrix, $\MAT{K}$ , for $P_1$ -Lagrange finite element method in 2d (see Elastic Stiffness Matrix)

Test 1: Computation of the Elastic Stiffness Matrix using the base, OptV1 and OptV2 versions : it gives errors and computation times

Test 2: Computation of the integral

$\int_{\Omega_h} \underline{\pmb{\epsilon}}^t(u) \underline{\pmb{\sigma}}(v)dq \approx \pmb{V}^t\mathbb{K} \pmb{U}$

where $\vecb{u}=(u_1,u_2)$ and $\vecb{v}=(v_1,v_2)$ are given 2d-vector functions and $\pmb{U}$ and $\pmb{V}$ are the vectors in $\R^{2\nq}$ defined by

if Num=0 or Num=2 (i.e. in global alternate basis $\mathcal{B}_a$ , see Assembly matrices (base, OptV1 and OptV2 versions) )

$\forall i\in\{1,\hdots,\nq\},\ U_{2i-1}=u_1(\q^i),\ U_{2i}=u_2(\q^i),\ \mbox{ and } \ V_{2i-1}=v_1(\q^i),\ \ V_{2i}=v_2(\q^i)$

if Num=1 or Num=3 (i.e. in global block basis $\mathcal{B}_b$ , see Assembly matrices (base, OptV1 and OptV2 versions) )

$\forall i\in\{1,\hdots,\nq\},\ U_{i}=u_1(\q^i),\ U_{i+\nq}=u_2(\q^i),\ \mbox{ and } \ V_{i}=v_1(\q^i),\ \ V_{i+\nq}=v_2(\q^i)$

Test 3: Ones retrieves the order 2 of $P_1$ -Lagrange integration

$|\int_{\Omega_h} \underline{\pmb{\epsilon}}^t(u) \underline{\pmb{\sigma}}(v) - \underline{\pmb{\epsilon}}^t(\Pi_h(u)) \underline{\pmb{\sigma}}(\Pi_h(v)) d\Omega| \leq C h^2$

Note

pyOptFEM.valid2D.validStiff2DP1.validStiffElas2DP1([Num=0, la=1.5, mu=0.5])¶

Parameters:	Num – (optional) Numbering choice. la – (optional) the first Lame coefficient in Hooke’s law, denoted by 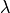$\lambda$ . mu – (optional) the second Lame coefficient in Hooke’s law, denoted by $\mu$ .

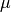pyOptFEM.valid2D.validStiffElas2DP1.validStiffElas2DP1(**kwargs)[source]: validation of elasticity stiffness matrix assembly functions

>>> from pyOptFEM.valid2D import validStiffElas2DP1
>>> validStiffElas2DP1()
**************************************************
*     2D StiffElas Assembling P1 validations     *
**************************************************
  Numbering Choice : global alternate numbering with local alternate numbering
-----------------------------------------
  Test 1: Matrices errors and CPU times
-----------------------------------------
    Matrix size           : (1922,1922)
    Error P1base vs OptV1 : 1.776357e-15
    Error P1base vs OptV2 : 2.664535e-15
    CPU times base (ref)  : 1.9251 (s)
    CPU times OptV1       : 0.2817 (s) - Speed Up X6.835
    CPU times OptV2       : 0.0098 (s) - Speed Up X195.725
----------------------------
  Test 1 (results): OK
----------------------------
-----------------------------------------------------
  Test 2: Validations by integration on [0,1]x[0,1]
-----------------------------------------------------
    function 0 :
      u(x,y)=[x - 2*y,x + y],
      v(x,y)=[x + 2*y,2*x - y],
           -> StiffElas error=8.704149e-14
    function 1 :
      u(x,y)=[x**2+2*y*x+y,-2*y**2+x**2+x-y],
      v(x,y)=[3*x*y+y**2+1,3*x**2-x*y+1],
           -> StiffElas error=3.916049e-03
    function 2 :
      u(x,y)=[x**3+2*y**2*x+y**2+x,y**3-2*x**2*y],
      v(x,y)=[2*x*y+y**3+x*y,3*x**3-2*x*y+x-1],
           -> StiffElas error=6.574856e-03
----------------------------
  Test 2 (results): OK
----------------------------
--------------------------------
  Test 3: Validations by order
--------------------------------
    functions 2:
      u(x,y)=['x**3+2*y**2*x+y**2+x', 'y**3-2*x**2*y'],
      v(x,y)=['2*x*y+y**3+x*y', '3*x**3-2*x*y+x-1'],
      lambda=1.500000, mu=0.500000
        Matrix size                          : (242,242)
        StiffElasAssemblingP1OptV2 CPU times : 0.002(s)
        Error                                : 5.767667e-02
        Matrix size                          : (882,882)
        StiffElasAssemblingP1OptV2 CPU times : 0.005(s)
        Error                                : 1.447542e-02
        Matrix size                          : (1922,1922)
        ...
        Matrix size                          : (20402,20402)
        StiffElasAssemblingP1OptV2 CPU times : 0.110(s)
        Error                                : 5.797263e-04

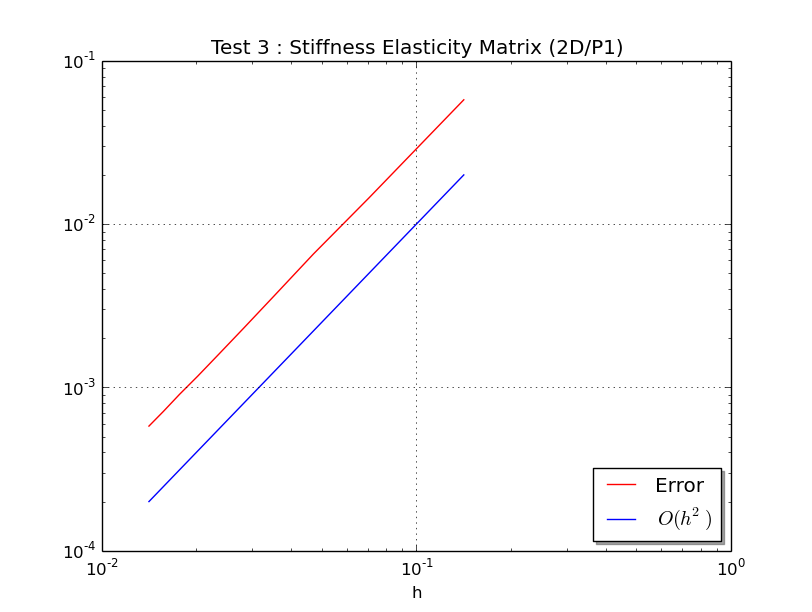
At last, this program plots this figure :

Figure 58: Graphical results of validStiffElas2DP1-Test 3

valid2D module¶

Mass Matrix ¶

Stiffness matrix ¶

Elastic Stiffness Matrix ¶

Table Of Contents

Previous topic

Next topic

This Page

Navigation

valid2D module¶

Mass Matrix¶

Stiffness matrix¶

Elastic Stiffness Matrix¶

Table Of Contents

Previous topic

Next topic

This Page

Quick search

Navigation

Mass Matrix ¶

Stiffness matrix ¶

Elastic Stiffness Matrix ¶