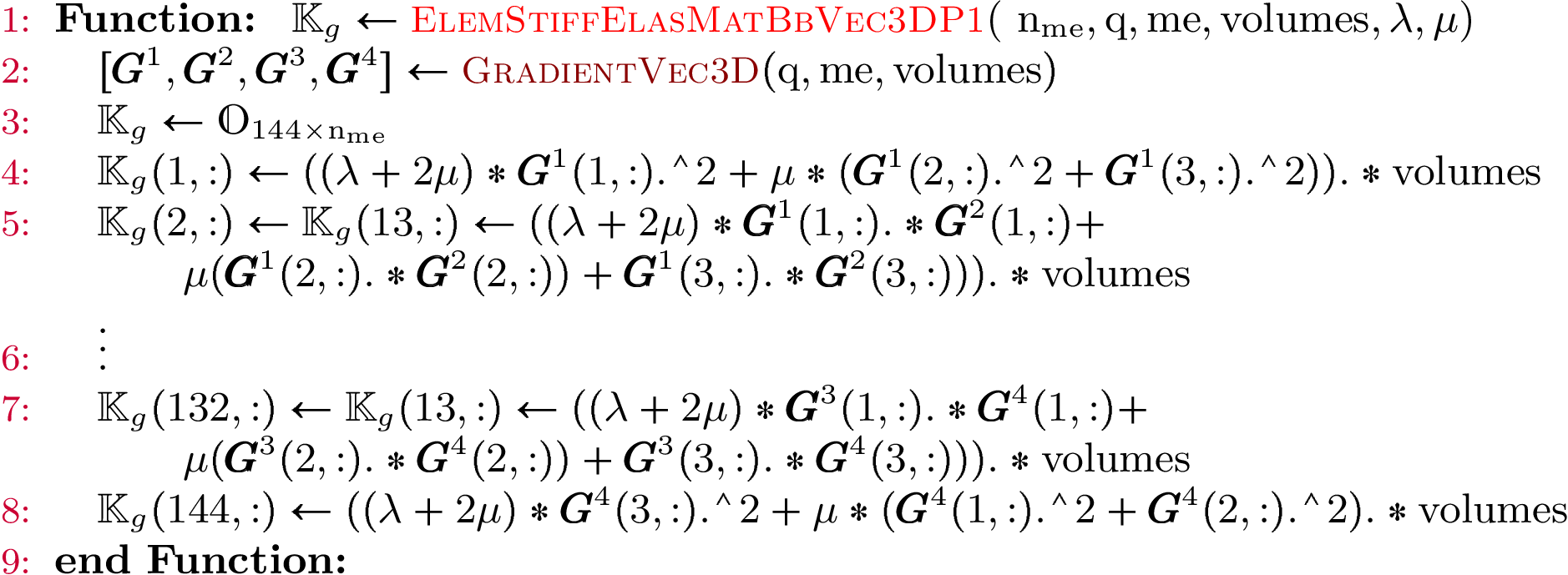FEM3D module¶
| Author: | Francois Cuvelier <cuvelier@math.univ-paris13.fr> |
|---|---|
| Date: | 15/09/2013 |
Contains functions to build some finite element matrices using 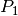 -Lagrange finite elements on a 3D mesh.
Each assembly matrix is computed by three differents versions called base,
OptV1 and OptV2 (see here)
-Lagrange finite elements on a 3D mesh.
Each assembly matrix is computed by three differents versions called base,
OptV1 and OptV2 (see here)
Contents
Assembly matrix (base, OptV1 and OptV2 versions)¶
Let 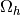 be a tetrahedral mesh of
be a tetrahedral mesh of 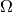 corresponding
to the following structure data:
corresponding
to the following structure data:
![\mbox{\begin{tabular}{lccll}
\hline
\textbf{name} & \textbf{type} & \textbf{dimension} & \textbf{description} & \textbf{Python}\\
\hline
$\nq$ & integer & 1 & number of vertices & \texttt{nq}\\
$\nme$ & integer & 1 & number of elements & \texttt{nme}\\
$\q$ & double & $3 \times {\nq}$ &
\begin{minipage}[t]{7.9cm}
array of vertices coordinates. $\q(\al,j)$ is the $\nu$-th coordinate of the $j$-th vertex,
$\al\in\{1,2,3\}$, $j\in\{1,\hdots,\nq\}.$
The $j$-th vertex will be also denoted by $\q^j$
\end{minipage}&
\begin{minipage}[t]{3cm}
\texttt{q} (transposed)\\
\texttt{q[j-1]} = $\q^j$
\end{minipage}\\
$\me$ & integer & $4 \times \nme$ &
\begin{minipage}[t]{7.9cm}
connectivity array. ${\me}(\jl,k)$ is the storage index of the $\beta$-th vertex
of the $k$-th element, in the array~$q$, for $\jl\in\{1,\hdots,4\}$ and $k\in\{1,\hdots,{\nme}\}$
\end{minipage}&\texttt{me} (transposed)\\
$\rm volumes$ & double & $1\times {\nme}$ &
\begin{minipage}[t]{7.9cm}
array of volumes. ${\rm volumes}(k)$ is the $k$-th tetrahedron volume,
$k\in\{1,\hdots,\nme\}$
\end{minipage}&\texttt{volumes}\\
\hline
\end{tabular}}](_images/math/cc16cf40bee8d694e1d96b522c2dff9e8317f5d2.png)
The 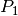 -Lagrange basis functions associated to
-Lagrange basis functions associated to 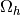 are denoted by
are denoted by 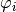 for all
for all 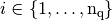 and are defined by
and are defined by
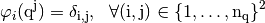
We also define the global alternate basis 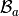 by
by
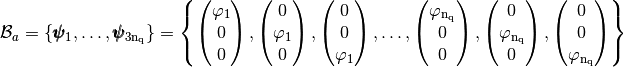
and the global block basis 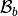 by
by
Mass Matrix¶
Assembly of the Mass Matrix by 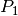 -Lagrange finite elements
using base, OptV1 and OptV2 versions respectively (see report).
The Mass Matrix
-Lagrange finite elements
using base, OptV1 and OptV2 versions respectively (see report).
The Mass Matrix 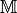 is given by
is given by
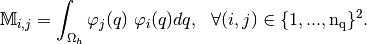
Note
generic syntax:
M = MassAssembling3DP1<version>(nq,nme,me,volumes)
- nq: total number of nodes of the mesh, also denoted by
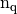 ,
, - nme: total number of tetrahedra, also denoted by
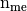 ,
, - me: Connectivity array, (nme,4) array,
- volumes: Array of tetrahedra volumes, (nme,) array,
- returns a Scipy CSC sparse matrix of size
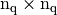
where <version> is base, OptV1 or OptV2
>>> from pyOptFEM.FEM3D import *
>>> Th=CubeMesh(5)
>>> Mbase = MassAssembling3DP1base(Th.nq,Th.nme,Th.me,Th.volumes)
>>> MOptV1= MassAssembling3DP1OptV1(Th.nq,Th.nme,Th.me,Th.volumes)
>>> print(" NormInf(Mbase-MOptV1)=%e " % NormInf(Mbase-MOptV1))
NormInf(Mbase-MOptV1)=1.734723e-18
>>> MOptV2= MassAssembling3DP1OptV2(Th.nq,Th.nme,Th.me,Th.volumes)
>>> print(" NormInf(Mbase-MOptV2)=%e " % NormInf(Mbase-MOptV2))
NormInf(Mbase-MOptV2)=1.734723e-18
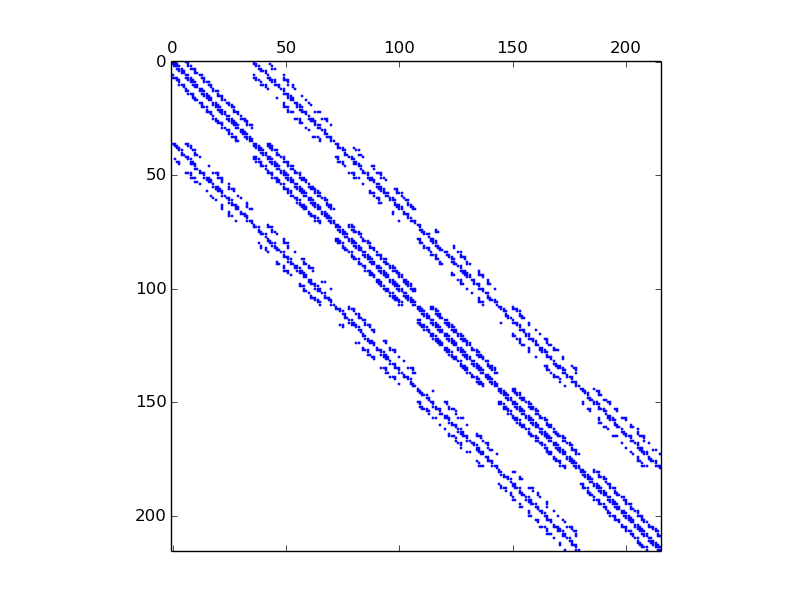
We can show sparsity of the Mass matrix :
Note
source code
- pyOptFEM.FEM3D.assembly.MassAssembling3DP1base(nq, nme, me, volumes)[source]
Assembly of the Mass Matrix by
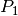 -Lagrange finite elements using base version (see report).
-Lagrange finite elements using base version (see report).
- pyOptFEM.FEM3D.assembly.MassAssembling3DP1OptV1(nq, nme, me, volumes)[source]
Assembly of the Mass Matrix by
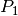 -Lagrange finite elements using OptV1 version (see report).
-Lagrange finite elements using OptV1 version (see report).
- pyOptFEM.FEM3D.assembly.MassAssembling3DP1OptV2(nq, nme, me, volumes)[source]
Assembly of the Mass Matrix by
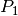 -Lagrange finite elements using OptV2 version (see report).
-Lagrange finite elements using OptV2 version (see report).
Stiffness Matrix¶
Assembly of the Stiffness Matrix by 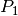 -Lagrange finite elements using base,
OptV1 and OptV2 versions respectively (see report).
The Stiffness Matrix
-Lagrange finite elements using base,
OptV1 and OptV2 versions respectively (see report).
The Stiffness Matrix 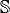 is given by
is given by
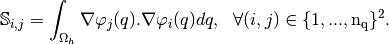
Note
generic syntax
- M=StiffAssembling3DP1<version>(nq,nme,q,me,volumes)
Compute the stiffness sparse matrix where <version> is base, OptV1 or OptV2
Parameters: - nq – total number of nodes of the mesh, also denoted by
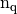 ,
, - nme – total number of tetrahedra, also denoted by
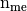 ,
, - q (numpy array of float) –
- array of vertices coordinates,
- (nq,3) array for base and OptV1 versions,
- (3,nq) array for OptV2 version,
- me (numpy array of int) –
- Connectivity array,
- (nme,4) array for base and OptV1 versions,
- (4,nme) array for OptV2 version,
- volumes (numpy array of floats,) – (nme,) array of tetrahedra volumes,
Returns: a Scipy CSC sparse matrix of size
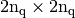
- nq – total number of nodes of the mesh, also denoted by
Benchmarks of theses functions are presented in Stiffness Matrix. We give a simple usage :
>>> from pyOptFEM.FEM3D import *
>>> Th=CubeMesh(5)
>>> Sbase = StiffAssembling3DP1base(Th.nq,Th.nme,Th.q,Th.me,Th.volumes)
>>> SOptV1= StiffAssembling3DP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.volumes)
>>> print(" NormInf(Sbase-SOptV1)=%e " % NormInf(Sbase-SOptV1))
NormInf(Sbase-SOptV1)=2.220446e-15
>>> SOptV2= StiffAssembling3DP1OptV2(Th.nq,Th.nme,Th.q,Th.me,Th.volumes)
>>> print(" NormInf(Sbase-SOptV2)=%e " % NormInf(Sbase-SOptV2))
NormInf(Sbase-SOptV2)=2.220446e-15
Note
source code
- pyOptFEM.FEM3D.assembly.StiffAssembling3DP1base(nq, nme, q, me, volumes)[source]
Assembly of the Stiffness Matrix by
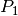 -Lagrange finite elements using base version (see report).
-Lagrange finite elements using base version (see report).
- pyOptFEM.FEM3D.assembly.StiffAssembling3DP1OptV1(nq, nme, q, me, volumes)[source]
Assembly of the Stiffness Matrix by
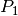 -Lagrange finite elements using OptV1 version (see report).
-Lagrange finite elements using OptV1 version (see report).
- pyOptFEM.FEM3D.assembly.StiffAssembling3DP1OptV2(nq, nme, q, me, volumes)[source]
Assembly of the Stiffness Matrix by
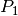 -Lagrange finite elements using OptV2 version (see report).
-Lagrange finite elements using OptV2 version (see report).
Elastic Stiffness Matrix¶
Assembly of the Elastic Stiffness Matrix by 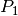 -Lagrange finite elements using base,
OptV1 and OptV2 versions respectively (see report).
The Elastic Stiffness Matrix
-Lagrange finite elements using base,
OptV1 and OptV2 versions respectively (see report).
The Elastic Stiffness Matrix 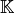 is given by
is given by
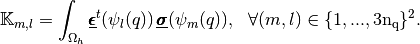
where 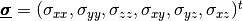 and
and
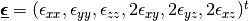 are the elastic stress and strain tensors respectively.
are the elastic stress and strain tensors respectively.
Note
generic syntax
- M=StiffElasAssembling3DP1<version>(nq,nme,q,me,volumes,la,mu,Num)
Compute the elastic stiffness sparse matrix where <version> is base, OptV1 or OptV2
Parameters: - nq – total number of nodes of the mesh,
- nme – total number of tetrahedrons,
- q (numpy array of float) –
- vertices coordinates,
- (nq,3) array for base and OptV1 versions,
- (3,nq) array for OptV2 version,
- me (numpy array of int) –
- connectivity array,
- (nme,4) array for base and OptV1 versions,
- (4,nme) array for OptV2 version,
- volumes (numpy array of floats,) – (nme,) array of tetrahedra volumes,
- la – the first Lame coefficient in Hooke’s law, denoted by
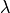 ,
, - mu – the second Lame coefficient in Hooke’s law, denoted by
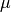 ,
, - Num –
- 0 global alternate numbering with local alternate numbering (classical method),
- 1 global block numbering with local alternate numbering,
- 2 global alternate numbering with local block numbering,
- 3 global block numbering with local block numbering.
Returns: a Scipy CSC sparse matrix of size
>>> from pyOptFEM.FEM3D import *
>>> Th=CubeMesh(5)
>>> Kbase = StiffElasAssembling3DP1base(Th.nq,Th.nme,Th.q,Th.me,Th.volumes,2,0.5,0)
>>> KOptV1= StiffElasAssembling3DP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.volumes,2,0.5,0)
>>> print(" NormInf(Kbase-KOptV1)=%e " % NormInf(Kbase-KOptV1))
NormInf(Kbase-KOptV1)=1.332268e-15
>>> KOptV2= StiffElasAssembling3DP1OptV2(Th.nq,Th.nme,Th.q,Th.me,Th.volumes,2,0.5,0)
>>> print(" NormInf(Kbase-KOptV2)=%e " % NormInf(Kbase-KOptV2))
NormInf(Kbase-KOptV2)=1.332268e-15
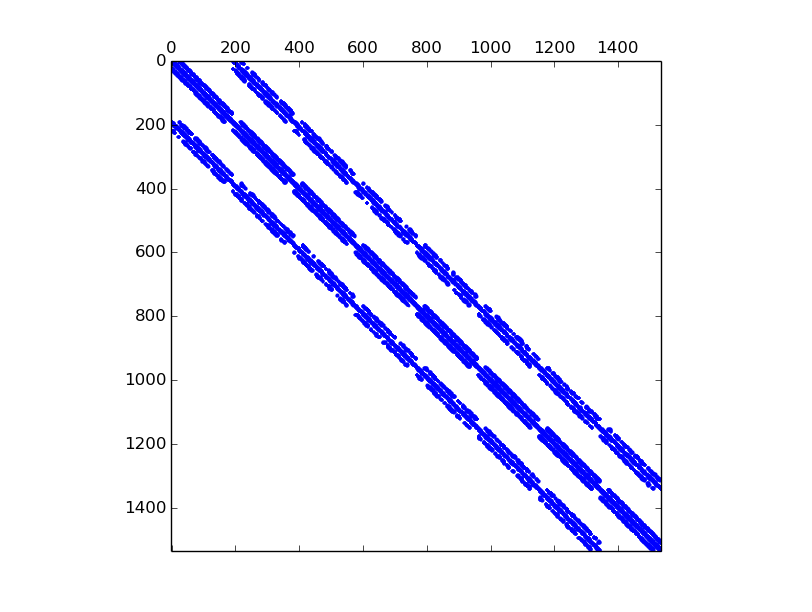
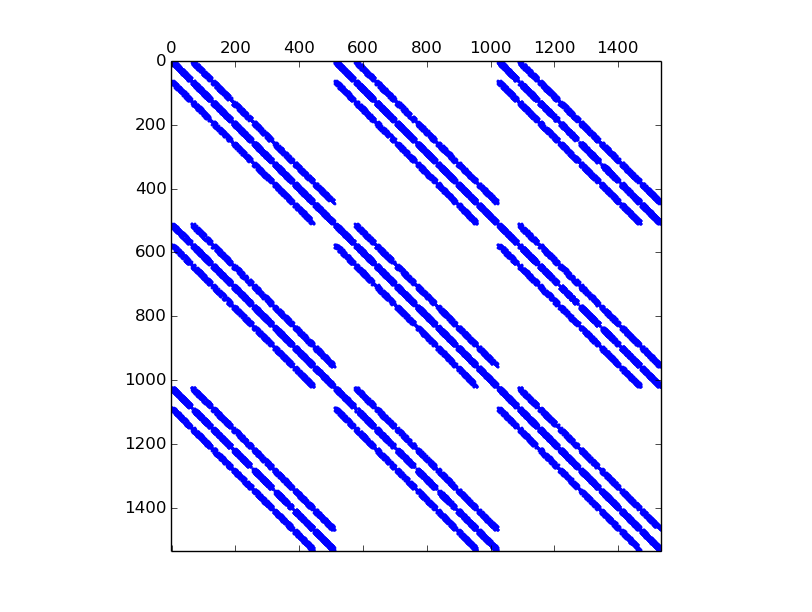
We now illustrate the consequences of the choice of the global basis on matrix sparsity
global alternate basis
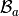 (Num=0 or Num=2)
(Num=0 or Num=2)>>> from pyOptFEM.FEM3D import * >>> Th=CubeMesh(5) >>> K0=StiffElasAssembling3DP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.volumes,2,0.5,0) >>> showSparsity(K0)
global block basis
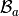 (Num=1 or Num=3)
(Num=1 or Num=3)>>> K3=StiffElasAssembling3DP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.volumes,2,0.5,3) >>> showSparsity(K3)
Note
source code
- pyOptFEM.FEM3D.assembly.StiffElasAssembling3DP1base(nq, nme, q, me, volumes, la, mu, Num)[source]
Assembly of the Elasticity Stiffness Matrix by
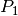 -Lagrange finite elements using base version (see report).
-Lagrange finite elements using base version (see report).
- pyOptFEM.FEM3D.assembly.StiffElasAssembling3DP1OptV1(nq, nme, q, me, volumes, la, mu, Num)[source]
Assembly of the Elasticity Stiffness Matrix by
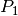 -Lagrange finite elements using OptV1 version (see report).
-Lagrange finite elements using OptV1 version (see report).
- pyOptFEM.FEM3D.assembly.StiffElasAssembling3DP1OptV2(nq, nme, q, me, volumes, la, mu, Num)[source]
Assembly of the Elasticity Stiffness Matrix by
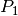 -Lagrange finite elements using OptV2 version (see report).
-Lagrange finite elements using OptV2 version (see report).
Element matrix (used by base and OptV1 versions)¶
Let 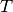 be a tetrahedron of volume
be a tetrahedron of volume 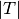 and with
and with 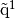 ,
, 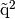 ,
,
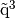 and
and 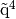 its four vertices. We denote by
its four vertices. We denote by
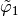 ,
, 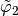 ,
, 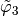 and
and
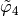 the
the 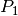 -Lagrange local basis functions such that
-Lagrange local basis functions such that 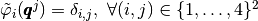 .
.
We also define the local alternate basis 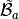 by
by
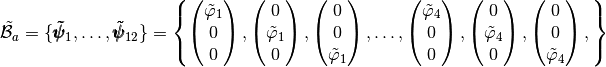
and the local block basis 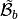 by
by
The elasticity tensor,  , obtained from Hooke’s law with an isotropic material,
defined with the Lamé parameters
, obtained from Hooke’s law with an isotropic material,
defined with the Lamé parameters 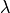 and
and 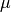 is given by
is given by
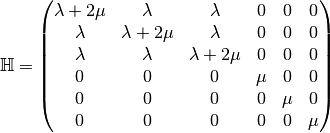
and, for a function 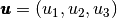 the strain tensors is given by
the strain tensors is given by

Element Elastic Stiffness Matrix¶
The element elastic stiffness matrix,
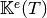 ,
for a given tetrahedron
,
for a given tetrahedron 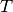 in the local alternate basis
in the local alternate basis 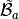 is defined by
is defined by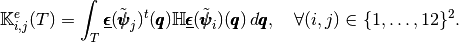
We also have
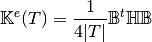
where
 is the elasticity tensor and
is the elasticity tensor and 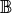 is a
is a 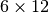 matrix defined by
matrix defined by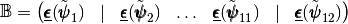
So in
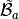 basis we obtain
basis we obtain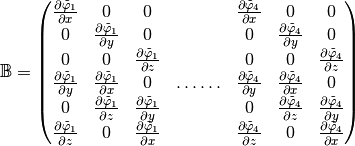
Note
source code
- pyOptFEM.FEM3D.elemMatrix.ElemStiffElasMatBa3DP1(ql, V, C)[source]¶
Returns the element elastic stiffness matrix
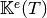 for a given tetrahedron
for a given tetrahedron 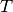 in the local alternate basis
in the local alternate basis 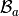
Parameters: - ql (
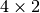 numpy array) – contains the four vertices of the tetrahedron,
numpy array) – contains the four vertices of the tetrahedron, - V (float) – volume of the tetrahedron
- H (
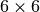 numpy array) – Elasticity tensor,
numpy array) – Elasticity tensor,  .
.
Returns: 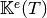 in
in 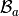 basis.
basis.Type : 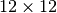 numpy array of floats.
numpy array of floats.- ql (
The element elastic stiffness matrix,
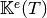 ,
for a given triangle
,
for a given triangle 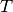 in the local block basis
in the local block basis 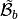 is defined by
is defined by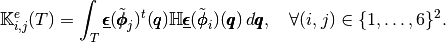
We also have
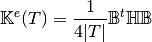
where
 is the elasticity tensor and
is the elasticity tensor and 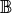 is a
is a 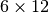 matrix defined by
matrix defined by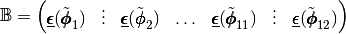
So in
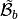 basis we obtain
basis we obtain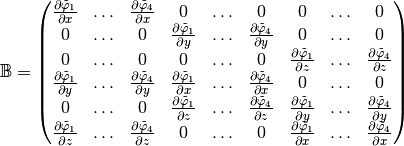
Note
source code
- pyOptFEM.FEM3D.elemMatrix.ElemStiffElasMatBb3DP1(ql, V, C)[source]¶
Returns the element elastic stiffness matrix
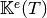 for a given tetrahedron
for a given tetrahedron 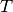 in the local block basis
in the local block basis 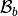
Parameters: - ql (
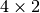 numpy array) – contains the four vertices of the tetrahedron,
numpy array) – contains the four vertices of the tetrahedron, - V (float) – volume of the tetrahedron
- H (
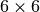 numpy array) – Elasticity tensor,
numpy array) – Elasticity tensor,  .
.
Returns: 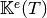 in
in 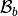 basis.
basis.Type :  numpy array of floats.
numpy array of floats.- ql (
Vectorized tools (used by OptV2 version)¶
Vectorized computation of basis functions gradients¶
By construction, the gradients of basis functions are constants on each element 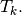 So, we denote,
So, we denote, 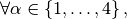 by
by 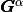 the
the 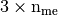 array defined,
array defined,
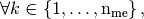 by
by
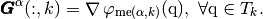
On 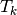 tetrahedra
we set
tetrahedra
we set
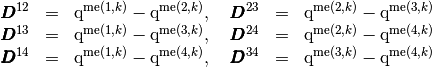
Then, we have
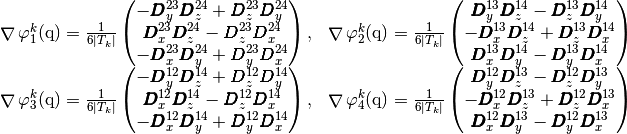
With these formulas, we obtain the vectorized algorithm given in Algorithm 26.
Algorithm 26
Vectorized element matrix (used by OptV2 version)¶
Element Mass Matrix¶
We have
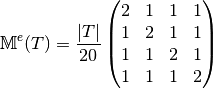
Then with 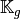 definition (see Section New Optimized assembly algorithm (OptV2 version)) , we obtain
definition (see Section New Optimized assembly algorithm (OptV2 version)) , we obtain
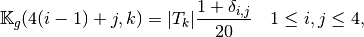
So the vectorized algorithm for 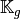 computation is simple and given in Algorithm 27.
computation is simple and given in Algorithm 27.
Algorithm 27
Note
- pyOptFEM.FEM3D.elemMatrixVec.ElemMassMat3DP1Vec(nme, volumes)[source]
Computes all the element Mass matrices
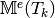 for
for 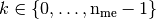
Parameters: volumes ( 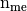 numpy array of floats) – volumes of all the mesh elements.
numpy array of floats) – volumes of all the mesh elements.Returns: a one dimensional numpy array of size 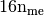
Element Stiffness Matrix¶
We have 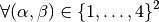
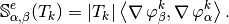
Using vectorized algorithm function 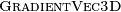 given in Algorithm 26, we obtain
the vectorized algorithm 28 for
given in Algorithm 26, we obtain
the vectorized algorithm 28 for 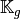 computation for the Stiffness matrix in 3d.
computation for the Stiffness matrix in 3d.
Algorithm 28
Note
- pyOptFEM.FEM3D.elemMatrixVec.ElemStiffMat3DP1Vec(nme, q, me, volumes)[source]
Computes all the element stiffness matrices
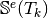 for
for 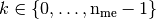
Parameters: - nme (int) – number of mesh elements,
- q (
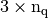 numpy array of floats) – mesh vertices,
numpy array of floats) – mesh vertices, - me (
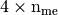 numpy array of integers) – mesh connectivity,
numpy array of integers) – mesh connectivity, - areas (
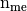 numpy array of floats) – areas of all the mesh elements.
numpy array of floats) – areas of all the mesh elements.
Returns: a one dimensional numpy array of size
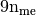
Element Elastic Stiffness Matrix¶
We define on the tetrahedron
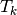 the local alternate basis
the local alternate basis 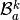 by
by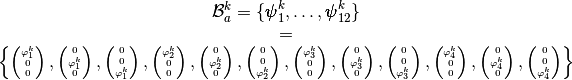
where
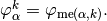 With notations of Presentation,
we have
With notations of Presentation,
we have 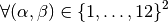
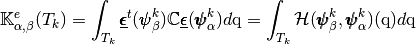
with,
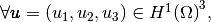
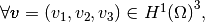 by
by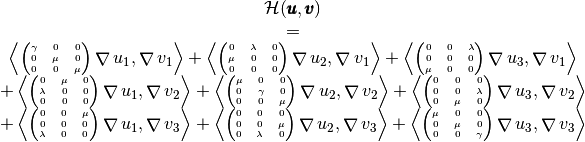
where
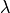 and
and 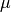 are the Lame coefficients and
are the Lame coefficients and 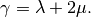
For example, we can explicitly compute the first two terms in the first column of
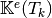 which are given by
which are given by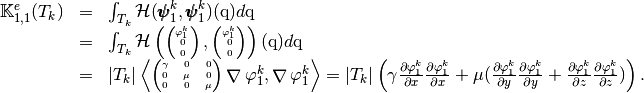
and
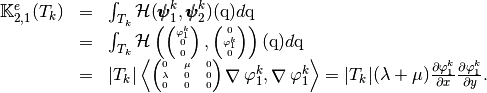
Using vectorized algorithm function
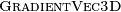 given in Algorithm 26, we obtain
the vectorized algorithm 29 for
given in Algorithm 26, we obtain
the vectorized algorithm 29 for 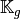 computation for the Elastic Stiffness matrix in 3d.
computation for the Elastic Stiffness matrix in 3d.Algorithm 29
Note
- pyOptFEM.FEM3D.elemMatrixVec.ElemStiffElasMatBa3DP1Vec(nme, q, me, volumes, la, mu)[source]
Computes all the element elastic stiffness matrices
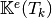 for
for 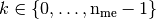 in local alternate basis.
in local alternate basis.Parameters: Returns: a (144*nme,) numpy array of floats.
We define on
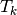 the local block basis
the local block basis 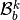 by
by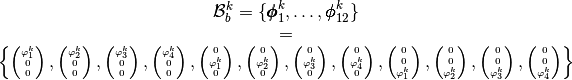
where
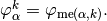
For example, using formula (?), we can explicitly compute the first two terms in the first column of
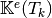 which are given by
which are given by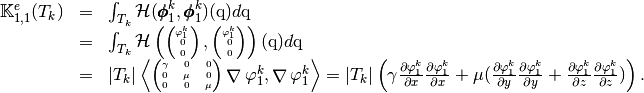
and
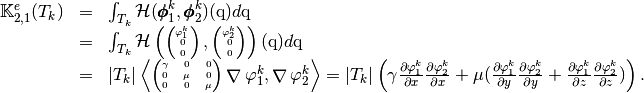
Using vectorized algorithm function
 given in Algorithm 26, we obtain
the vectorized algorithm 30 for
given in Algorithm 26, we obtain
the vectorized algorithm 30 for 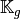 computation for the Elastic Stiffness matrix in 3d.
computation for the Elastic Stiffness matrix in 3d.Algorithm 30
Note
- pyOptFEM.FEM3D.elemMatrixVec.ElemStiffElasMatBb3DP1Vec(nme, q, me, volumes, L, M)[source]
Compute all the element elastic stiffness matrices,
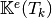 for
for 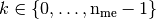 in local block basis.
in local block basis.Parameters: Returns: a (144*nme,) numpy array of floats.
Mesh¶
- class pyOptFEM.FEM3D.mesh.CubeMesh(N, **kwargs)[source]¶
Creates meshes of the unit cube
![[0,1]^3](_images/math/84d989f1815cde65061abef404e8efdf2a02a3c1.png) . Class attributes are :
. Class attributes are :nq, total number of mesh vertices (points), also denoted
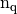 .
.nme, total number of mesh elements (tetrahedra in 3d),
version, mesh structure version,
q, Numpy array of vertices coordinates, dimension (nq,3) (version 0) or (3,nq) (version 1).
q[j] (version 0) or q[:,j] (version 1) are the three coordinates of the
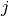 -th vertex,
-th vertex, 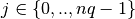
me, Numpy connectivity array, dimension (nme,4) (version 0) or (4,nme) (version 1).
me[k] (version 0) or me[:,k] (version 1) are the storage index of the four vertices of the
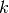 -th tetrahedron in the array q of vertices coordinates,
-th tetrahedron in the array q of vertices coordinates, 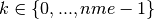 .
.volumes, Array of mesh elements volumes, (nme,) Numpy array.
volumes[k] is the volume of
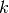 -th tetrahedron, k in range(0,nme)
-th tetrahedron, k in range(0,nme)
Parameters: N – number of points on each edge of the cube optional parameter : version=0 or version=1
- class pyOptFEM.FEM3D.mesh.getMesh(filename, **kwargs)[source]¶
Reads a medit mesh from file meshfile. Class attributes are :
nq, total number of mesh vertices (points), also denoted
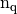 .
.nme, total number of mesh elements (tetrahedra in 3d),
version, mesh structure version,
q, Numpy array of vertices coordinates, dimension (nq,3) (version 0) or (3,nq) (version 1).
q[j] (version 0) or q[:,j] (version 1) are the three coordinates of the
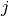 -th vertex,
-th vertex, 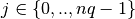
me, Numpy connectivity array, dimension (nme,4) (version 0) or (4,nme) (version 1).
me[k] (version 0) or me[:,k] (version 1) are the storage index of the four vertices of the
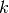 -th tetrahedron in the array q of vertices coordinates,
-th tetrahedron in the array q of vertices coordinates, 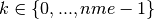 .
.volumes, Array of mesh elements volumes, (nme,) Numpy array.
volumes[k] is the volume of
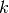 -th tetrahedron, k in range(0,nme)
-th tetrahedron, k in range(0,nme)
Parameters: meshfile – medit mesh file optional parameter : version=0 or version=1
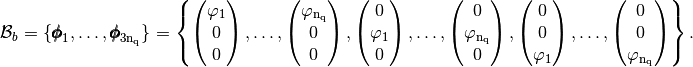
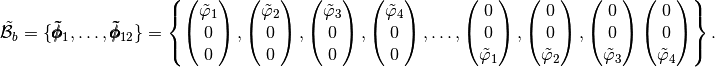
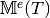 for the tetrahedron
for the tetrahedron 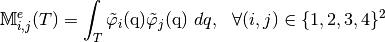
 numpy array of floats.
numpy array of floats. ,
for the
,
for the 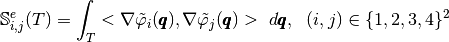
 numpy array) – the four vertices of the tetrahedron,
numpy array) – the four vertices of the tetrahedron,
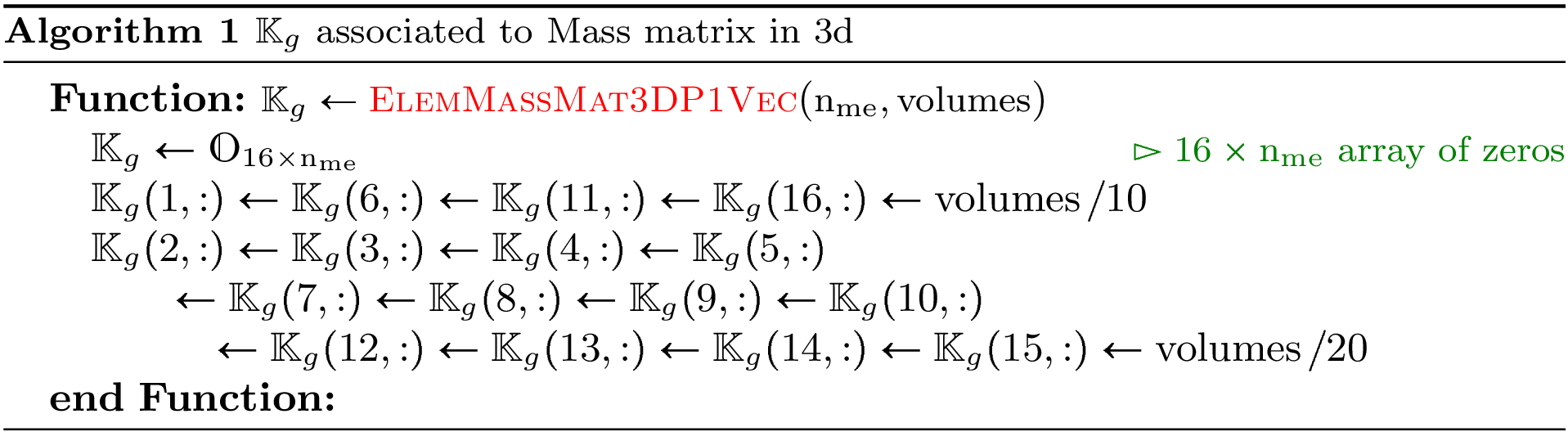
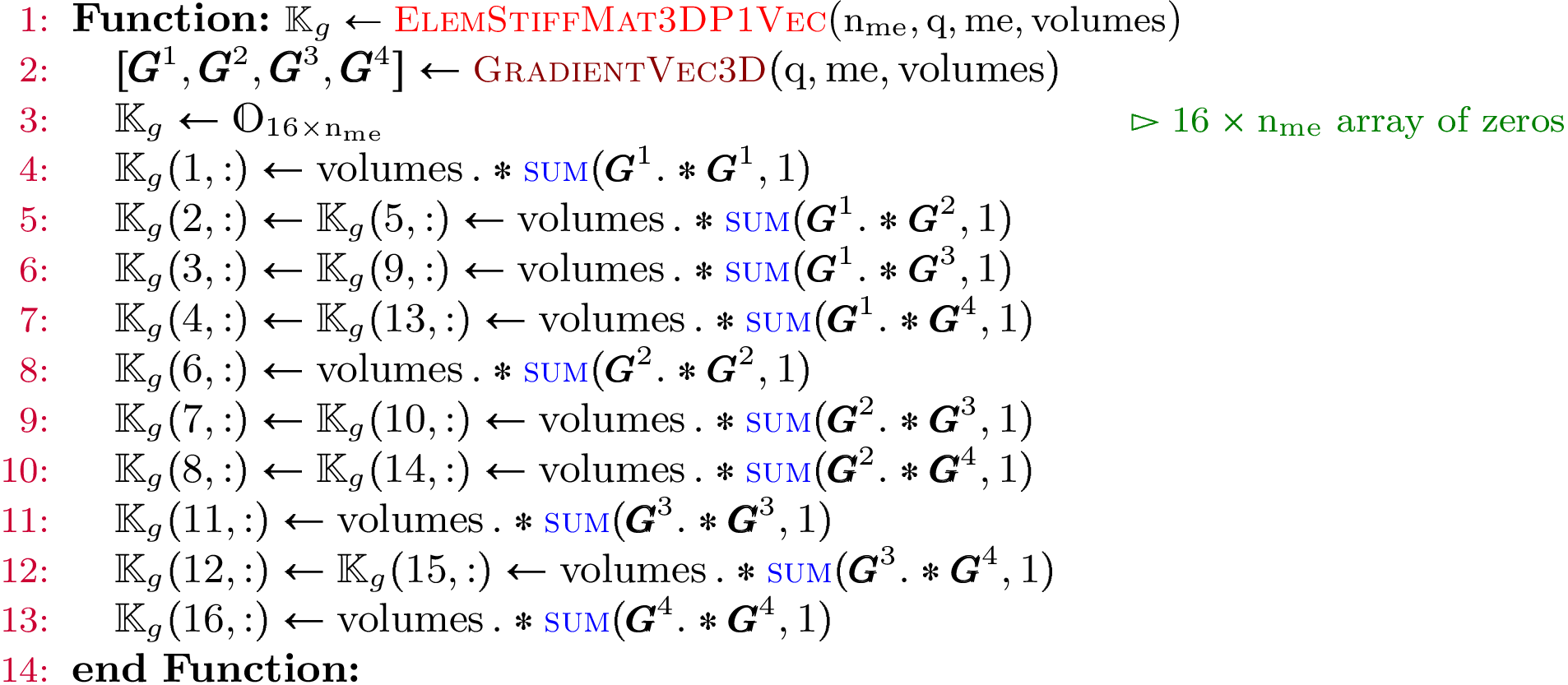
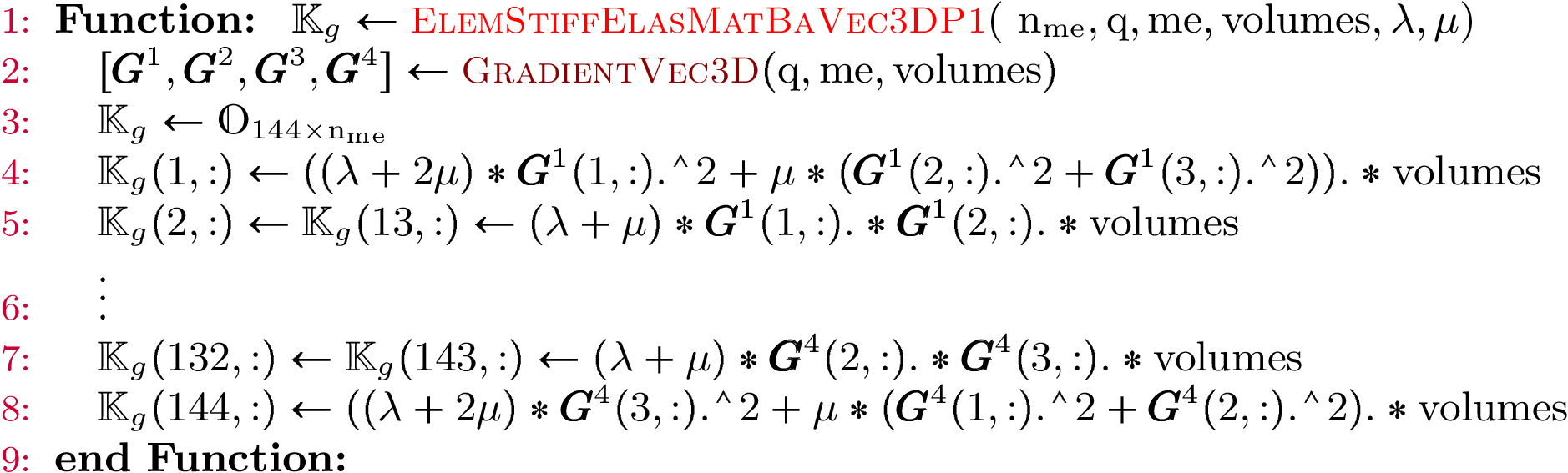
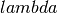 Lame parameter,
Lame parameter,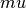 Lame parameter.
Lame parameter.