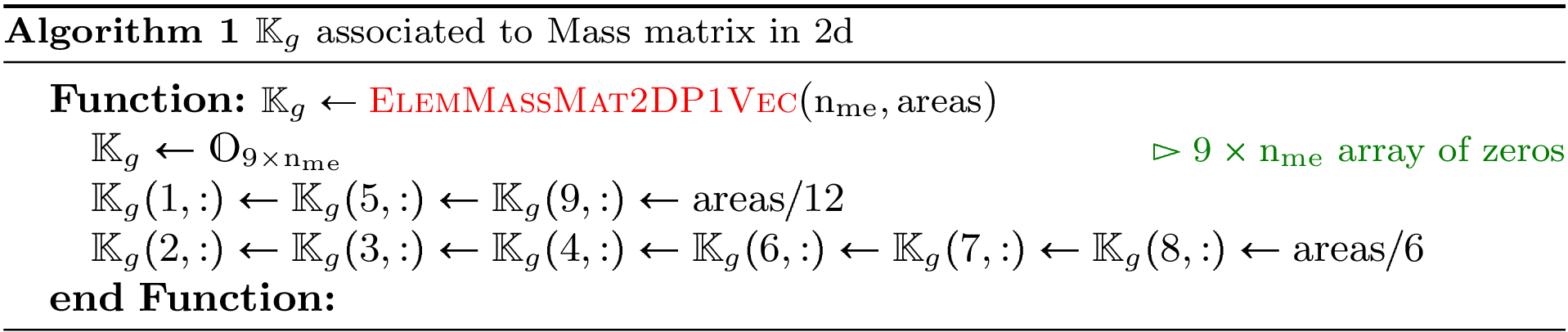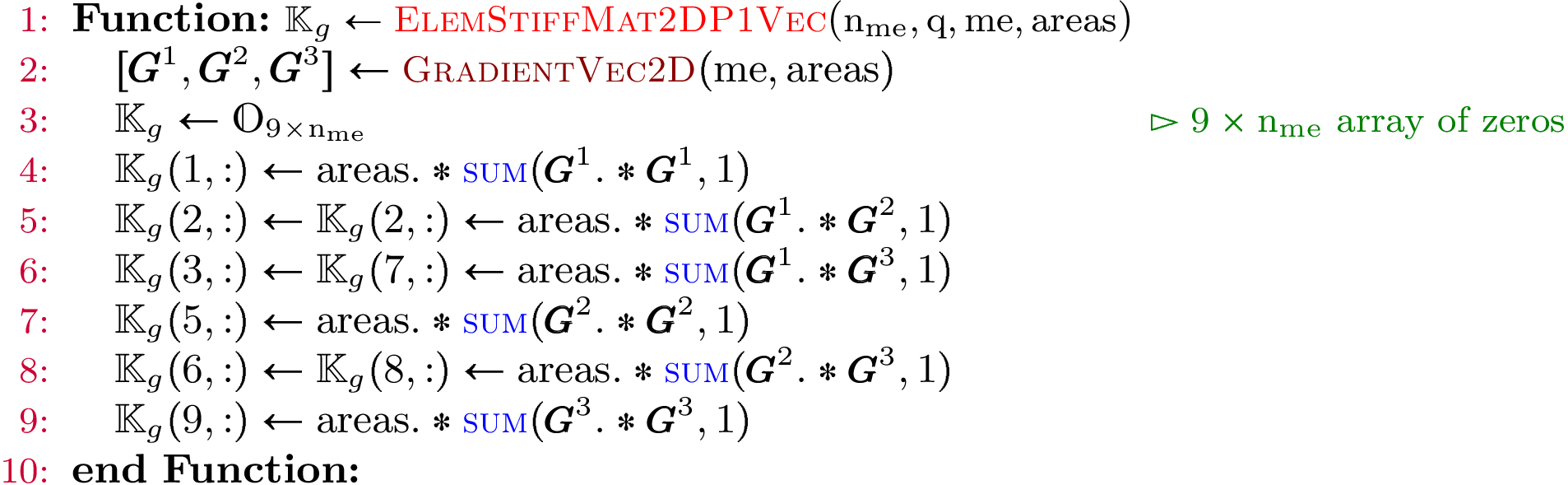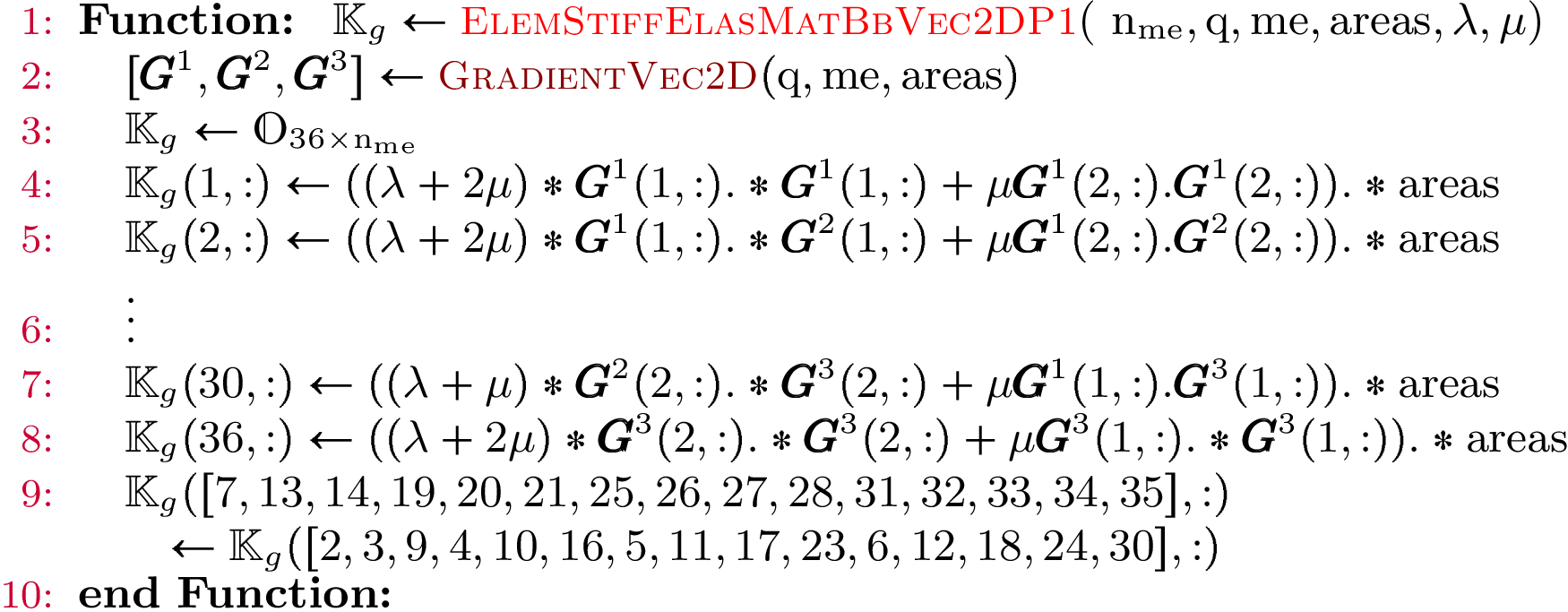Element Mass Matrix¶

We have

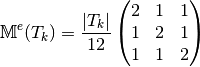
$\mathbb{M}^e(T_k) =\frac{|T_k|}{12}\begin{pmatrix} 2 & 1 & 1\\ 1 & 2 & 1\\ 1 & 1 & 2 \end{pmatrix}$

Then with 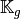$\MAT{K}_g$ definition (see Section New Optimized assembling algorithm (version OptV2)) , we obtain

$\MAT{K}_g(3(i-1)+j,k)=|T_k|\frac{1+\delta_{i,j}}{12} \quad 1\le i,j \le 3,$

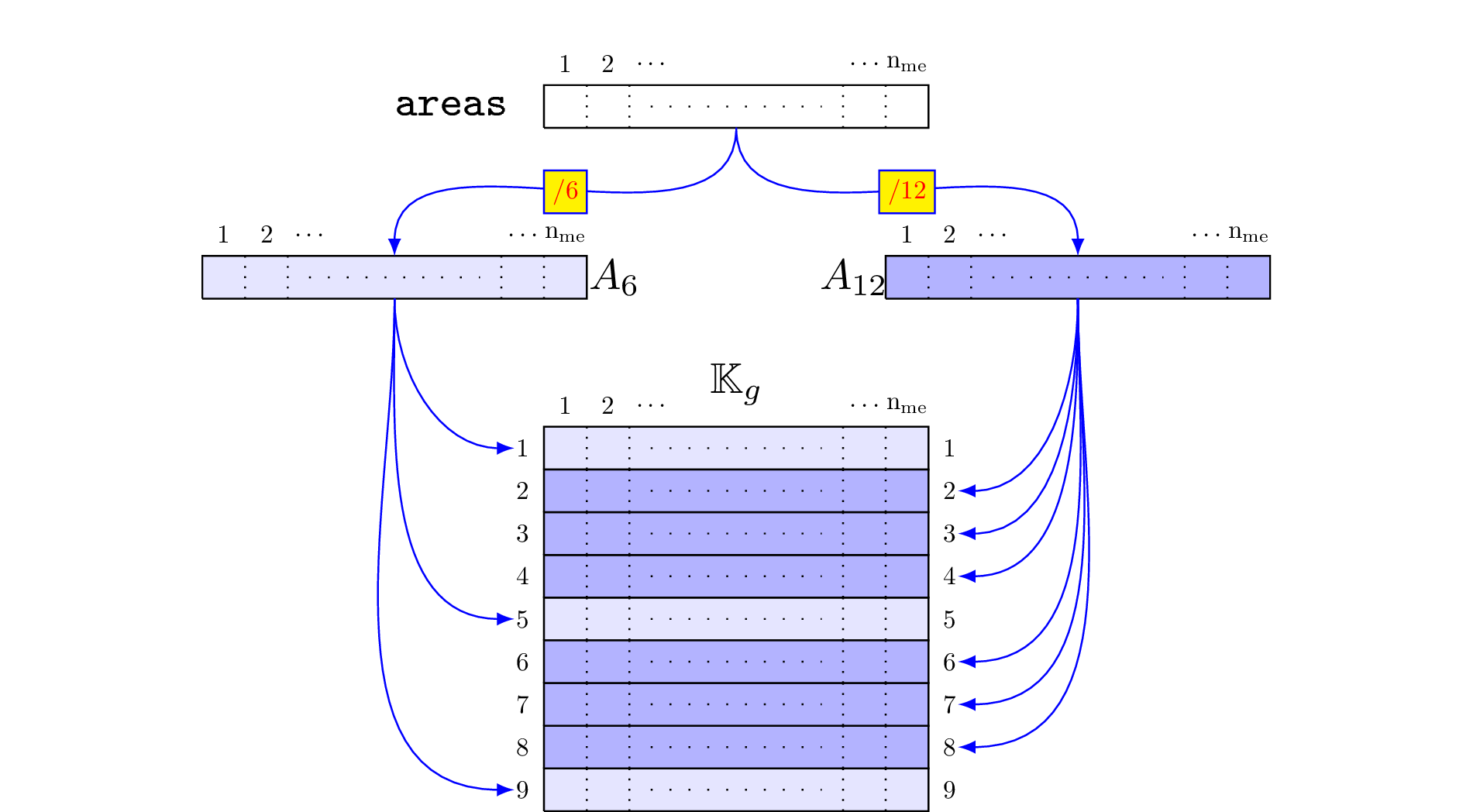
We represent in figure 135 the corresponding row-wise operations.

Figure 135: Build of $\mathbb{K}_g$ associated to 2d Mass matrix in

So the vectorized algorithm for $\mathbb{K}_g$ computation is simple and given in Algorithm 136.

Algorithm 136

Figure 136: Vectorized algorithm for $\mathbb{K}_g$ associated to 2d Mass matrix

Note

pyOptFEM.FEM2D.elemMatrixVec.ElemMassMat2DP1Vec(areas)[source]

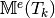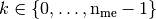
Compute all the elementaries Mass matrices, $\mathbb{M}^e(T_k)$ for $k\in\{0,\hdots,\nme-1\}$

Parameters:	areas ( 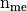$\nme$ numpy array of floats) – areas of all the mesh elements.
Returns:	a one dimensional numpy array of size 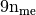$9 \nme$

Element Stiffness Matrix¶

We have 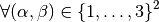$\forall (\il,\jl)\in\ENS{1}{3}^2$

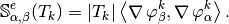
$\mathbb{S}_{\il,\jl}^e(T_k)= |T_k| \DOT{\GRAD\BasisFunc_{\jl}^k}{\GRAD\BasisFunc_{\il}^k}.$

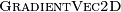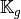Using vectorized algorithm function $\FNametxt{GradientVec2D}$ given in Algorithm 134, we obtain the vectorized algorithm 137 for $\mathbb{K}_g$ computation of the Stiffness matrix in 2d.

Algorithm 137

Figure 137: Vectorized algorithm for $\mathbb{K}_g$ associated to 2d Stiffness matrix

Note

pyOptFEM.FEM2D.elemMatrixVec.ElemStiffMat2DP1Vec(nme, q, me, areas)[source]

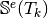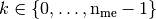
Compute all the elementaries Stiff matrices, $\mathbb{S}^e(T_k)$ for $k\in\{0,\hdots,\nme-1\}$

Parameters:	nme (int) – number of mesh elements, q ( 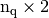$\nq\times 2$ numpy array of floats) – mesh vertices, me ( 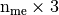$\nme\times 3$ numpy array of integers) – mesh connectivity, areas ( 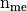$\nme$ numpy array of floats) – areas of all the mesh elements.
Returns:	a one dimensional numpy array of size $9 \nme$

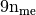
Element Stiffness Elasticity Matrix¶

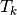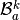We define on $T_k$ the local alternate basis $\mathcal{B}_a^k$ by

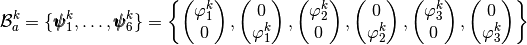
$\mathcal{B}_a^k=\{\BasisFuncTwoD_1^k,\hdots,\BasisFuncTwoD_6^k\}=\left\{ \begin{pmatrix} \BasisFunc_1^k \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ \BasisFunc_1^k \end{pmatrix}, \begin{pmatrix} \BasisFunc_2^k \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ \BasisFunc_2^k\end{pmatrix}, \begin{pmatrix} \BasisFunc_3^k \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ \BasisFunc_3^k \end{pmatrix} \right\}$

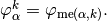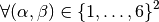
where $\BasisFunc_\il^k=\BasisFunc_{\me(\il,k)}.$ With notations of Presentation, we have $\forall (\il,\jl) \in \ENS{1}{6}^2$

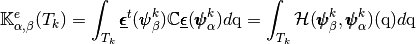
$\StiffElasElem_{\il,\jl}(T_k)= \int_{T_k} \Odv^t(\BasisFuncTwoD^k_\jl) \mathbb{C}\Odv(\BasisFuncTwoD^k_\il)d\q= \int_{T_k} \mathcal{H}(\BasisFuncTwoD^k_\jl,\BasisFuncTwoD^k_\il)(\q)d\q$

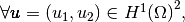
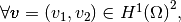
with, $\forall \vecb{u}=(u_1,u_2)\in\HUnD{\DOM}^2,$ $\forall \vecb{v}=(v_1,v_2)\in\HUnD{\DOM}^2,$

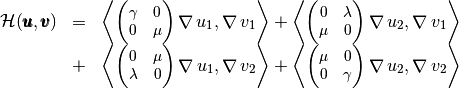
(1) $\begin{array}{lcl} \mathcal{H}(\vecb{u},\vecb{v})&=&{\footnotesize \DOT{\begin{pmatrix} \gamma & 0\\ 0 & \mu \end{pmatrix}\GRAD u_1 }{\GRAD v_1} +\DOT{\begin{pmatrix} 0 & \lambda\\ \mu & 0 \end{pmatrix}\GRAD u_2 }{\GRAD v_1}}\\ &+&{\footnotesize\DOT{\begin{pmatrix} 0 & \mu\\ \lambda & 0 \end{pmatrix}\GRAD u_1 }{\GRAD v_2}+ \DOT{\begin{pmatrix} \mu & 0\\ 0 &\gamma\end{pmatrix}\GRAD u_2 }{\GRAD v_2}} \end{array}$

For example, we can compute explicitely the first two terms in the first column of 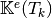$\StiffElasElem(T_k)$ which are given by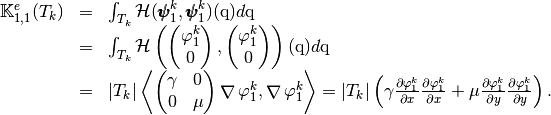

$\begin{array}{lcl} \StiffElasElem_{1,1}(T_k)&=&\int_{T_k} \mathcal{H}(\BasisFuncTwoD^k_{1},\BasisFuncTwoD^k_{1})(\q)d\q\\ &=&\int_{T_k} \mathcal{H}\left( \begin{pmatrix} \BasisFunc^k_{1}\\ 0 \end{pmatrix}, \begin{pmatrix} \BasisFunc^k_{1}\\ 0 \end{pmatrix} \right)(\q)d\q\\ &=&|T_k| \DOT{\begin{pmatrix} \gamma & 0\\ 0 & \mu \end{pmatrix}\GRAD \BasisFunc^k_{1} }{\GRAD \BasisFunc^k_{1}} =|T_k|\left(\gamma\DP{\BasisFunc^k_{1}}{x}\DP{\BasisFunc^k_{1}}{x}+\mu\DP{\BasisFunc^k_{1}}{y}\DP{\BasisFunc^k_{1}}{y}\right). \end{array}$

and

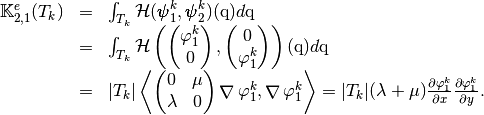
$\begin{array}{lcl} \StiffElasElem_{2,1}(T_k)&=&\int_{T_k} \mathcal{H}(\BasisFuncTwoD^k_{1},\BasisFuncTwoD^k_{2})(\q)d\q\\ &=&\int_{T_k} \mathcal{H}\left( \begin{pmatrix} \BasisFunc^k_{1}\\ 0 \end{pmatrix}, \begin{pmatrix} 0\\ \BasisFunc^k_{1} \end{pmatrix} \right)(\q)d\q\\ &=&|T_k| \DOT{\begin{pmatrix} 0 & \mu\\ \lambda & 0 \end{pmatrix}\GRAD \BasisFunc^k_{1} }{\GRAD \BasisFunc^k_{1}} =|T_k|(\lambda+\mu)\DP{\BasisFunc^k_{1}}{x}\DP{\BasisFunc^k_{1}}{y}. \end{array}$

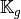Using vectorized algorithm function $\FNametxt{GradientVec2D}$ given in Algorithm 134, we obtain the vectorized algorithm 137 for $\mathbb{K}_g$ computation of the Elasticity Stiffness matrix in 2d.

Algorithm 138

Figure 138: Vectorized algorithm for $\mathbb{K}_g$ associated to 2d Elasticity Stiffness matrix

Note

pyOptFEM.FEM2D.elemMatrixVec.ElemStiffElasMatBaVec2DP1(nme, q, me, areas, L, M)[source]

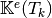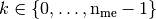Compute all the elementaries Stiffness elasticity matrices, $\mathbb{K}^e(T_k)$ for $k\in\{0,\hdots,\nme-1\}$ in local alternate basis.

Parameters:	nme (int) – number of mesh elements, q (`(2,nq)` numpy array of floats) – mesh vertices, me (`(3,nme)` numpy array of integers) – mesh connectivity, areas (`(nme,)` numpy array of floats) – areas of all the mesh elements. L – the 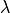$\lambda$ Lame parameter, L – the 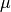$\mu$ Lame parameter.
Returns:	a `(36nme,)` numpy* array of floats.

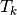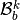We define on $T_k$ the local block basis $\mathcal{B}_b^k$ by

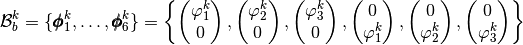
$\mathcal{B}_b^k=\{\BasisFuncTwoDB_1^k,\hdots,\BasisFuncTwoDB_6^k\}=\left\{ \begin{pmatrix} \BasisFunc_1^k \\ 0 \end{pmatrix}, \begin{pmatrix} \BasisFunc_2^k \\ 0 \end{pmatrix}, \begin{pmatrix} \BasisFunc_3^k \\ 0 \end{pmatrix}, \begin{pmatrix} 0 \\ \BasisFunc_1^k \end{pmatrix}, \begin{pmatrix} 0 \\ \BasisFunc_2^k\end{pmatrix}, \begin{pmatrix} 0 \\ \BasisFunc_3^k \end{pmatrix} \right\}$

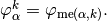
where $\BasisFunc_\il^k=\BasisFunc_{\me(\il,k)}.$

For example, using formula (1), we can explicitly compute the first two terms in the first column of 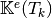$\StiffElasElem(T_k)$ which are given by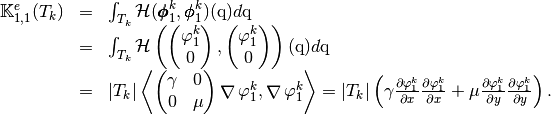

$\begin{array}{lcl} \StiffElasElem_{1,1}(T_k)&=&\int_{T_k} \mathcal{H}(\BasisFuncTwoDB^k_{1},\BasisFuncTwoDB^k_{1})(\q)d\q\\ &=&\int_{T_k} \mathcal{H}\left( \begin{pmatrix} \BasisFunc^k_{1}\\ 0 \end{pmatrix}, \begin{pmatrix} \BasisFunc^k_{1}\\ 0 \end{pmatrix} \right)(\q)d\q\\ &=&|T_k| \DOT{\begin{pmatrix} \gamma & 0\\ 0 & \mu \end{pmatrix}\GRAD \BasisFunc^k_{1} }{\GRAD \BasisFunc^k_{1}} =|T_k|\left(\gamma\DP{\BasisFunc^k_{1}}{x}\DP{\BasisFunc^k_{1}}{x}+\mu\DP{\BasisFunc^k_{1}}{y}\DP{\BasisFunc^k_{1}}{y}\right). \end{array}$

and

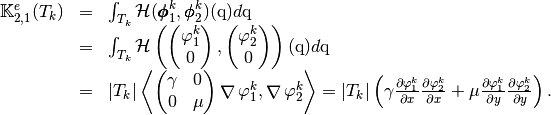
$\begin{array}{lcl} \StiffElasElem_{2,1}(T_k)&=&\int_{T_k} \mathcal{H}(\BasisFuncTwoDB^k_{1},\BasisFuncTwoDB^k_{2})(\q)d\q\\ &=&\int_{T_k} \mathcal{H}\left( \begin{pmatrix} \BasisFunc^k_{1}\\ 0 \end{pmatrix}, \begin{pmatrix} \BasisFunc^k_{2}\\ 0 \end{pmatrix} \right)(\q)d\q\\ &=&|T_k| \DOT{\begin{pmatrix} \gamma & 0\\ 0 & \mu \end{pmatrix}\GRAD \BasisFunc^k_{1} }{\GRAD \BasisFunc^k_{2}} =|T_k|\left(\gamma\DP{\BasisFunc^k_{1}}{x}\DP{\BasisFunc^k_{2}}{x}+\mu\DP{\BasisFunc^k_{1}}{y}\DP{\BasisFunc^k_{2}}{y} \right). \end{array}$

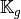Using vectorized algorithm function $\FNametxt{GradientVec2D}$ given in Algorithm 134, we obtain the vectorized algorithm 139 for $\mathbb{K}_g$ computation of the Elasticity Stiffness matrix in 2d.

Algorithm 139

Figure 139: Vectorized algorithm for $\mathbb{K}_g$ associated to 2d Elasticity Stiffness matrix

Note

pyOptFEM.FEM2D.elemMatrixVec.ElemStiffElasMatBbVec2DP1(nme, q, me, areas, L, M)[source]

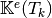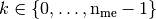Compute all the elementaries Stiffness elasticity matrices, $\mathbb{K}^e(T_k)$ for $k\in\{0,\hdots,\nme-1\}$ in local block basis.

Parameters:	nme (int) – number of mesh elements, q (`(2,nq)` numpy array of floats) – mesh vertices, me (`(3,nme)` numpy array of integers) – mesh connectivity, areas (`(nme,)` numpy array of floats) – areas of all the mesh elements. L – the 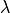$\lambda$ Lame parameter, L – the 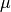$\mu$ Lame parameter.
Returns:	a `(36nme,)` numpy* array of floats.

Element Mass Matrix¶

Element Stiffness Matrix¶

Element Stiffness Elasticity Matrix¶

Table Of Contents

This Page

Navigation

Element Mass Matrix¶

Element Stiffness Matrix¶

Element Stiffness Elasticity Matrix¶

Table Of Contents

This Page

Quick search

Navigation