 |
OptFEM2DP1 Toolbox
V1.2b3
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 2D
|
 |
OptFEM2DP1 Toolbox
V1.2b3
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 2D
|
Computation of the element stiffness elasticity matrix for 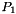 -Lagrange method. The method for numbering the degrees of freedom is local alternate numbering (classical method)
More...
-Lagrange method. The method for numbering the degrees of freedom is local alternate numbering (classical method)
More...
Go to the source code of this file.
Functions | |
| function Elem = | ElemStiffElasMatP1Ba (q1, q2, q3, area, lambda, mu) |
Computation of the element stiffness elasticity matrix for 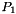 -Lagrange method. The method for numbering the degrees of freedom is local alternate numbering (classical method) -Lagrange method. The method for numbering the degrees of freedom is local alternate numbering (classical method) | |
Computation of the element stiffness elasticity matrix for 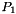 -Lagrange method. The method for numbering the degrees of freedom is local alternate numbering (classical method)
-Lagrange method. The method for numbering the degrees of freedom is local alternate numbering (classical method)
Definition in file ElemStiffElasMatP1Ba.m.
| function Elem = ElemStiffElasMatP1Ba | ( | q1, | |
| q2, | |||
| q3, | |||
| area, | |||
| lambda, | |||
| mu | |||
| ) |
Computation of the element stiffness elasticity matrix for 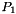 -Lagrange method. The method for numbering the degrees of freedom is local alternate numbering (classical method)
-Lagrange method. The method for numbering the degrees of freedom is local alternate numbering (classical method)
Example:
q1=[0;0];q2=[1;0];q3=[0;1];
area=1/2.;
lambda=1.; mu=1.;
KElem=ElemStiffElasMatP1Ba(q1,q2,q3,area,lambda,mu);| q1 | array of coordinates of the first point of the triangle |
| q2 | array of coordinates of the second point of the triangle |
| q3 | array of coordinates of the third point of the triangle |
| area | triangle area |
| lambda | first Lame coefficient in Hooke's law |
| mu | second Lame coefficient in Hooke's law |
| Elem | element stiffness elasticity matrix, 6-by-6 matrix |
Definition at line 17 of file ElemStiffElasMatP1Ba.m.