 |
OptFEM2DP1 Toolbox
V1.2b3
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 2D
|
 |
OptFEM2DP1 Toolbox
V1.2b3
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 2D
|
Initialization of the Mesh structure for a square domain. More...
Go to the source code of this file.
Functions | |
| function Th = | SquareMesh (N) |
| Initialization of the Mesh structure for a square domain. | |
Initialization of the Mesh structure for a square domain.
Definition in file SquareMesh.m.
| function Th = SquareMesh | ( | N | ) |
Initialization of the Mesh structure for a square domain.
Square domain is ![$[0,1]\times[0,1]$](form_38.png) .
.
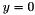
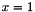
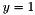
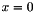
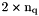 array.
array. 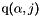 is the
is the 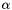 -th coordinate of the
-th coordinate of the 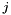 -th vertex,
-th vertex, 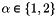 and
and 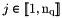 me: Connectivity array,
me: Connectivity array, 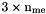 array.
array. 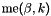 is the storage index of the
is the storage index of the 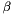 -th vertex of the
-th vertex of the 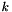 -th triangle in the array
-th triangle in the array 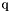 of vertices coordinates,
of vertices coordinates, 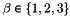 and
and 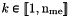 . ql: Array of vertices labels,
. ql: Array of vertices labels, 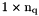 array. mel: Array of elements labels,
array. mel: Array of elements labels, 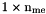 array. be: Connectivity array for boundary edges,
array. be: Connectivity array for boundary edges, 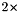 array.
array.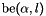 is the storage index of the
is the storage index of the 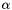 -th vertex of the
-th vertex of the 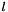 -th edge in the array
-th edge in the array 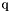 of vertices coordinates,
of vertices coordinates, 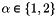 and
and 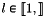 . bel: Array of boundary edges labels,
. bel: Array of boundary edges labels, 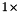 array. nq: total number of vertices, also denoted by
array. nq: total number of vertices, also denoted by 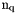 nme: total number of elements, also denoted by
nme: total number of elements, also denoted by 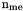 nbe: total number of boundary edges, also denoted by
nbe: total number of boundary edges, also denoted by  areas: Array of areas,
areas: Array of areas, 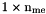 array. areas(k) is the area of the
array. areas(k) is the area of the 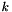 -th triangle. lbe: Array of edges lengths,
-th triangle. lbe: Array of edges lengths, 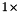 array.
array. 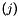 is the length of the
is the length of the 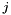 -th edge.
-th edge.| N | integer, number of elements on a boundary |
| Th | mesh structure |
Definition at line 17 of file SquareMesh.m.