 |
OptFEM2DP1 Toolbox
V1.2b3
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 2D
|
 |
OptFEM2DP1 Toolbox
V1.2b3
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 2D
|
Assembly of the Stiffness Elasticity Matrix by 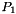 -Lagrange finite elements using "OptV1" version (see report).
More...
-Lagrange finite elements using "OptV1" version (see report).
More...
Go to the source code of this file.
Functions | |
| function K = | StiffElasAssemblingP1OptV1 (nq, nme, q, me, areas, lambda, mu, Num) |
Assembly of the Stiffness Elasticity Matrix by 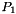 -Lagrange finite elements using "OptV1" version (see report). -Lagrange finite elements using "OptV1" version (see report). | |
Assembly of the Stiffness Elasticity Matrix by 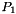 -Lagrange finite elements using "OptV1" version (see report).
-Lagrange finite elements using "OptV1" version (see report).
Definition in file StiffElasAssemblingP1OptV1.m.
| function K = StiffElasAssemblingP1OptV1 | ( | nq, | |
| nme, | |||
| q, | |||
| me, | |||
| areas, | |||
| lambda, | |||
| mu, | |||
| Num | |||
| ) |
Assembly of the Stiffness Elasticity Matrix by 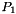 -Lagrange finite elements using "OptV1" version (see report).
-Lagrange finite elements using "OptV1" version (see report).
The Stiffness Elasticity Matrix is given by
![\[\StiffElas_{m,l}=\int_{\DOMH} \Odv^t(\BasisFuncTwoD_m) \Ocv(\BasisFuncTwoD_l)dT, \ \forall (m,l)\in\ENS{1}{2\,\nq}^2,\]](form_60.png)
where 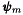 are
are 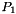 -Lagrange vector basis functions. Here
-Lagrange vector basis functions. Here 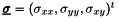 and
and 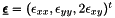 are the elastic stress and strain tensors respectively.
are the elastic stress and strain tensors respectively.
Th=SquareMesh(10);
lambda=1; mu=1;
Num = 0;
KK=StiffElasAssemblingP1OptV1(Th.nq,Th.nme,Th.q,Th.me,Th.areas,lambda,mu,Num);| nq | total number of nodes in the mesh, also denoted by 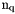 . . |
| nme | total number of triangles, also denoted by 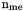 . . |
| q | Array of vertices coordinates, 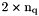 array. array. 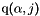 is the is the 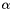 -th coordinate of the -th coordinate of the 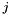 -th vertex, -th vertex, 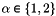 and and 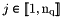 |
| me | Connectivity array, 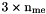 array. array. 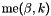 is the storage index of the is the storage index of the 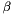 -th vertex of the -th vertex of the 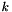 -th triangle in the array -th triangle in the array 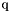 , , 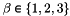 and and 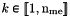 . . |
| areas | Array of areas, 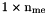 array. areas(k) is the area of the array. areas(k) is the area of the 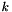 -th triangle. -th triangle. |
| lambda | the first Lame coefficient in Hooke's law |
| mu | the second Lame coefficient in Hooke's law |
| Num |
|
| K | 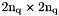 stiffness elasticity sparse matrix stiffness elasticity sparse matrix |
Definition at line 17 of file StiffElasAssemblingP1OptV1.m.