

ANR SAT
Higher structures in Algebra and Topology
 |
 ANR SAT
|

|
|---|---|---|
Members
|
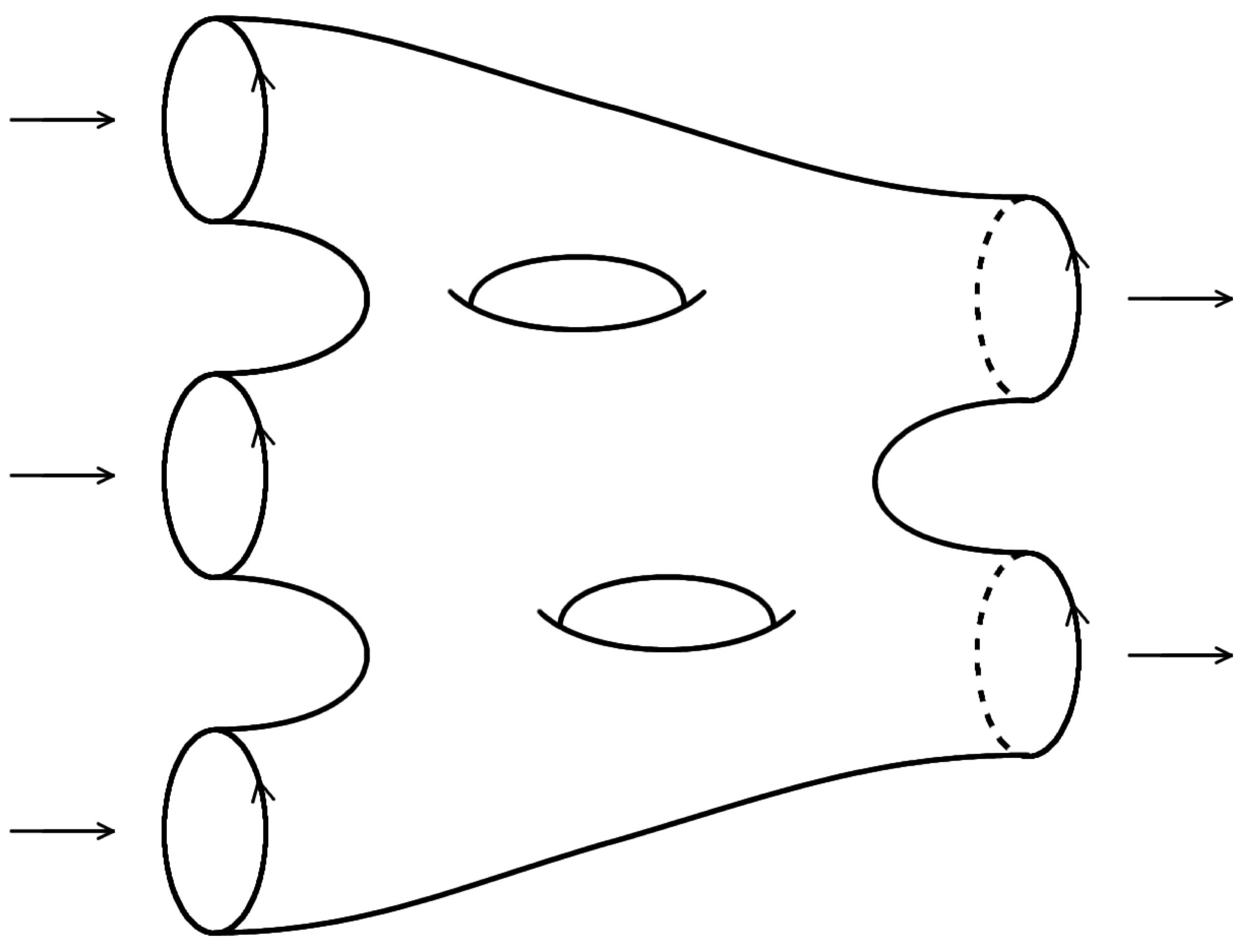
The present ANR project is a program of fundamental research in mathematics, more precisely in algebra and topology. Algebra. The theory of categories has proven to be a valuable algebraic tool to state and to organize the results in many areas in mathematics. In the same way, the notion of an operad, which emerged from the study of iterated loop spaces in the early 1970's, now plays a structural role by organizing the many operations with several inputs acting on the various objects in algebra, geometry, topology and mathematical physics. Higher algebra. At the end of the last century, it appeared clearly that the introduction of higher algebraic notions was necessary in order to encode higher structures naturally appearing in mathematical problems. Homotopy theory provides us with natural phenomena whose description requires higher maps, that is some notion of higher category. In the same way, the algebraic notion of an operad, while already used to describe homotopy algebras, was proved to be a too strict notion, e.g. for the purposes of deformation theory. After a long period of research in algebra and topology, the theory of higher structures gave rise recently to radically new and manageable notions, like infinity-categories, homotopy algebras and homotopy operads, which make possible the study of some unsolved questions like formality theorems (Kontsevich) and cobordism hypothesis (Lurie), for instance. Field theories. In an attempt to provide well established mathematical definitions to objects studied in field theory in physics, several renowned mathematicians introduced the notions of topological field theories, cohomological field theories and conformal field theories using categorical or operadic structures on geometrical objects: smooth manifolds with boundary (Atiyah), algebraic curves with marked points (Kontsevich--Manin), and Riemann surfaces with holomorphic punctures (Segal) respectively. Present project. This project consists in new foundational developments of high algebra directed toward the resolution of problems in the topological study of field theories. It proposes first to enrich one step further the theory of higher structures with new models, like a suitable notion of symmetric operad up to homotopy and a good notion of infinity-cooperad. Then it aims at applying these new methods to the mathematical study of field theories, like En-algebras, factorization algebras, topological field theories, cohomological field theories, vertex algebras and conformal field theories. |
Program founded by the Agence nationale de la recherche
|
 |
 |
