Analyse Topologique des Données
Responsable : Grégory Ginot
| Formation | M2 mathématiques des données
|
| Semestre | 1 |
| Bloc | Outils mathématiques pour le traitement et l'analyse des données |
| Enseignants | Cours : Grégory Ginot, Ian Morilla : |
| Crédits | 4 ECTS |
| Horaires | 21h de cours + 21h de TD/TP |
| Validation | Contrôle continu+examen |
Présentation
Ce cours aura pour vocation de donner une introduction à l'analyse topologique des données (TDA) en mettant l'accent sur les idées sous-jacentes et sur l'un de ses outils fondamentaux, l'homologie persistante. La TDA est un domaine récent ayant eu pour but de rendre effectifs, implémentables et manipulables, les outils de la topologie algébrique. L'idée sous-jacente à la TDA est d'utiliser les invariants de la topologie algébrique pour classifier ces données, les comparer, trouver des caractéristiques et signatures d'un certain type de données. Parmi les nombreuses applications concrètes : on peut citer la reconnaissance de formes et l’analyse d’images qui ont permis de classifier des bactéries et des neurones (spectroscopie moléculaire) ou d’identifier certaines formes de cancer (IRM).
Voici les points qui pourront être abordés :
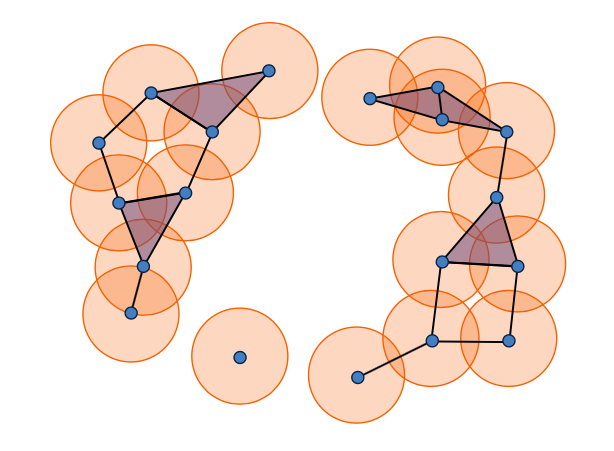
Nuages de points et simplexes : une idée clé de la TDA est d'associer à un nuage de point un complexe simplicial approximant l'espace dont le nuage est une discrétisation. Les complexes simpliciaux sont une donnée combinatoire encodant la géométrie de simplexes (ou polytopes) que l'on recolle sur leurs sous-faces. On expliquera ces données, leur réalisation et comment on encode en pratique ces objets: complexes de Cech (théorique) et de Rips (pratique). On fera bien entendu le lien entre ces constructions.
Homologie des complexes simpliciaux : pour comprendre un complexe simplicial à petite déformation près, on introduira ses invariants topologiques naturels donné par ses groupes d'homologie. On expliquera sa construction et on donnera ses propriétés importantes permettant de les calculer, leur invariance par homotopie. On verra en TD des algorithmes pour déterminer ces invariants.
Homologie persistante et codes barres : l'homologie persistante est associée à des espaces ou complexes simpliciaux filtrés comme ceux donnés par les nuages de points. On expliquera comment encoder des invariants combinatoires de ces structures obtenus en considérant l'évolution des classes d'homologie. Ces invariants sont appelés les codes barres.
Homologie persistante associées à des fonctions : on expliquera comment on introduit également des notions d'homologie persistante associée à des fonctions sur un espace compact; notions similaire à la théorie de Morse. En pratique ces constructions sont utilisées pour étudier des mesures obtenues ou des notions de distance dans les mesures.
Distances d'entrelacement et bottleneck : pour comparer différents jeux de données, on utilise une (pseudo)métrique sur les codes barres associés. On donnera leurs contructions et principales propriétés encodées par les théorèmes de stabilité.
Interprétation des distances et inférence topologique : on donnera un aperçu de l'utilisation pratique des outils précédents pour étudier des données, différencier et classifier des discrétisations.