Dernière modification avril 2015

Thématiques principales

1. La plupart de mes travaux de recherche concernent les Systèmes Dynamiques en petites dimension (homéomorphismes de surfaces, flots en dimension 3).  Je m’intéresse aux propriétés topologiques, géométriques, et parfois ergodiques, de ces systèmes. 
   

2. Je m’intéresse également à certaines questions mathématiques, de nature géométrique ou dynamiques, motivées par la Relativité Générale.
   

Ces deux thématiques se rejoignent parfois. Ainsi, j’ai étudié la dynamique des espaces-temps spatialement homogènes (ou espaces-temps de Bianchi), dont l’étude se ramène à celle d’un champ de vecteurs polynomial en dimension 4.

1. J’ai aussi consacré un temps important à des projets concernant l’histoire des mathématiques. Avec 14 collègues, nous avons essayé de retracer le chemin qui, tout au long du XIXème siècle, à mené au Théorème d’Uniformisation des Surfaces de Riemann. Nous étudions maintenant les mémoires dans lesquels Poincaré a mis sur pied la Topologie Algébrique.

Quelques problèmes sur lesquels j’ai travaillé

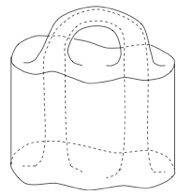
Difféomorphismes hyperboliques des surfaces et flots hyperboliques en dimension 3. Un difféomorphisme est Cr-structurellement stable si tout difféomorphisme proche en topologie Cr a la même dynamique à conjugaison topologique près. Robbin, Robinson, Mañé et Hayashi ont caractérisé les difféomorphismes et les flots C1 structurellement stables. La propriété clé est l’hyperbolicité, d’où l’appellation difféomorphismes et flots hyperboliques. Dans ma thèse, j’ai classé les difféomorphismes hyperboliques des surfaces. Bonatti et Langevin avait montré que la dynamique globale d’un tel difféomorphisme est caractérisée par une information combinatoire finie. J’ai déterminé quelles combinatoires abstraites correspondent effectivement à un difféomorphisme structurellement stable de surface. J’ai également décrit un algorithme permettant de décidé si deux combinatoires abstraites correspondent au même difféomorphisme. Les flots structurellement stables en dimension 3 constituent un généralisation naturelle des difféomorphismes hyperboliques des surfaces ; on gagne essentiellement une beaucoup plus grande richesse dans la topologie des espaces sous-jacents. Avec C. Bonatti, j’ai décrit une variété à bord «la plus simple possible» qui porte un flot hyperbolique de combinatoire donnée. Avec J. Vieitez et C. Bonatti, j’ai montré (par une construction explicite) que toute combinatoire abstraite correspond à un flot hyperbolique sur une variété compacte de dimension 3.

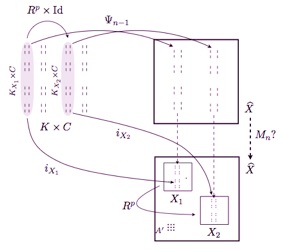
Pseudo-rotations. On sait depuis les travaux de Poincaré et Denjoy que la dynamique d’un homéomorphisme du cercle est déterminée en bonne partie par la simple donné du nombre rotation de cet homéomorphisme, qui mesure la vitesse asymptotique à laquelle les orbites tournent autour du cercle. La construction du nombre de rotation se généralise au homéomorphismes des surfaces, même si on aboutit non plus à un seul nombre, mais plutôt à une partie de H1(S,R) où S est la surface considérée. Une pseudo-rotation est un homéomorphisme de l’anneau ou du tore dont l’ensemble de rotation est réduit à un seul point. La question naturelle qui se pose alors est : à quel point une pseudo-rotation ressemble-t-elle à la «vraie» rotation de même angle ? Avec S. Crovisier et F. Le Roux, nous avons montré que si f est une pseudo-rotation, alors la rotation de même angle appartient à l’adhérence de la classe de conjugaison de f. Nous avons également construit des pseudo-rotations avec des dynamiques très riches. Par exemple, nous avons montré qu’il existe des pseudo-rotations du tore T2 minimales uniquement ergodiques, mais d’entropie topologique positive.

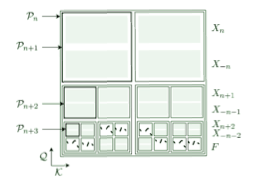
Réalisation de dynamiques mesurées par des homéomorphismes de surfaces. Un système dynamique mesuré (inversible) est la donnée d’une bijection bi-mesurable T d’un espace mesurable X, et d’un mesure de probabilité m que T laisse invariante. Comme tout application obtenu par un procédé de construction plus ou moins explicite est mesurable, il est facile de construire des systèmes dynamique mesurés. Cependant, de nombreux systèmes dynamique qui apparaissent naturellement en mathématiques ou dans d’autre sciences ont des propriétés de continuité : ce sont des homéomorphisme d’ensemble de Cantor, des difféomorphismes ou des flots sur des variétés. Il est alors naturel de se  demander si tout système dynamique mesuré est réalisable par un homéomorphisme d’un espace topologique, ou un difféomorphisme de variété. La question est essentiellement règlée en ce qui concerne les ensembles de Cantor, grâce au théorème de Jewett-Krieger. Par contre, elle est largement ouverte sur les variété, si on cherche des réalisation uniquement ergodiques. Avec S. Crovisier et F. Le Roux, nous avons montré que tout système dynamique mesuré ergodique qui possède une valeur propre irrationnelle dans son spectre est réalisable par un homéomorphisme minimal uniquement ergodique du tore de dimension 2.

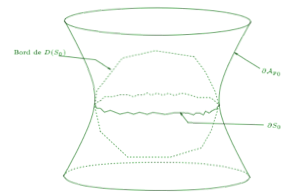
Fonctions temps spéciales sur certains espace-temps. Un des principes de la théorie de la Relativité est qu’il n’existe pas de temps absolu : chaque observateur a un temps propre. Ce principe est cependant local : en Relativité Générale, il se peut que, pour des raisons globales, il existe une mesure du temps (une fonction temps) privilégiée. Cette fonction temps est souvent de nature géométrique : par exemple si un espace-temps est feuilleté par des hypersurfaces spatiales à courbure moyenne constante, ces hypersurfaces sont souvent les niveaux d’une fonction temps (appelée fonction temps CMC). Une telle fonction est automatiquement unique par le principe du maximum. Avec T. Barbot et A. Zeghib, nous nous sommes intéressés aux espaces-temps à courbure constante. Ceux-ci ont bien sûr une géométrie locale triviale, mais il peuvent avoir une topologie et une géométrie globale complexe. Avec L. Andersson, T. Barbot, et A. Zeghib nous avons montré que presque tous les espaces-temps globalement hyperboliques maximaux spatialement compacts à courbure constante admettent des fonctions temps CMC uniques. Avec T. Barbot et A. Zeghib, nous avons ensuite montré un résultat analogue en dimension 3, pour des fonctions temps de Gauss, c’est-à-dire des fonctions temps dont les niveaux sont à courbure de Gauss constante. Nous avons réussi à prouver que la géométrie des fonctions temps CMC est comparable (bi-lipschitz) à celle de la fonction temps cosmologique. Notre but était de montrer que la géométrie limite des niveaux, quand on s’éloigne vers le passé, était la même pour les diverse fonctions temps canoniques, tendant ainsi à montrer que l’on peut ainsi définir un espace métrique qui serait la «singularité initiale». Cet espace métrique a d’ailleurs, dans les cas que nous considérons, une géométrie fort compliquée, puisque c’est le quotient de l’arbre duale d’une lamination géodésique par une action qui n’est nullement propre. Mehdi Belraouti a récemment amélioré ce résultat.

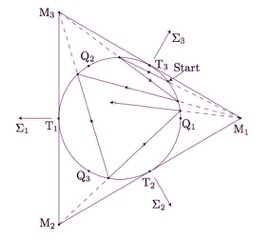
Espaces-temps de Bianchi. Les espaces-temps de Bianchi sont les espace-temps spatialement homogènes (mais non-isotropes). Autrement dit, ce sont des variété lorentziennes de la forme (M,g) où M est le produit d’un intervalle I de la droite réelle et d’un groupe de Lie G de dimension 3, et où la métrique g s’écrit -dt2+gt où gt est une métrique riemannienne invariante à gauche sur {t}xG. Il a été conjecturé il y a bien longtemps par Misner d’une part, et Belinskii, Kalatnikov et Lifschitz que les espaces-temps de Bianchi avait un comportement chaotique au voisinage de leur singularité initiale (au moins lorsque G est SO(3) ou SL(2,R)). J’ai réussi à montrer un résultat allant dans ce sens : il existe des espaces-temps de Bianchi qui ont un comportement oscillatoire au voisinage de leur singularité initiale, et ce comportement dépend de manière très sensible des conditions initiales. De plus, la preuve permet d’affirmer que ces espaces-temps sont asymptotiquement silencieux : d’un point de vue physique, ceci signifie que deux observateurs n’ont pas pu échanger d’information arbitrairement près de la singularité initiale. Ceci répond négativement à une conjecture de Misner.  M. Georgi, J. Harterich, S. Liebscher et K. Webster ont montré un résultat similaire au mien (bien que formellement disjoint) simultanément. Ces résultats ont ensuite été très vite améliorés par M. Reiterer et E. Trubowitz. Depuis peu, T. Dutilleul travaille sur le sujet sous ma direction.

Projets auxquels j’ai participé

1. Projet ACI Structures géométriques et trous noirs, 2003-2006. Responsable du projet : T. Barbot.
   

2. Projet ANR Geodycos, 2006-2010. Responsable du projet : T. Barbot.
   

3. Projet ANR Symplexe, 2006-2010. Responsable du projet : P. Le Calvez.
   

4. Je n’étais pas membre officiellement du projet DynNonHyp (porteurs : C. Bonatti, J. Buzzi et S. Crovisier), mais j’ai assisté à des rencontres et bénéficié à plusieurs reprise de sn soutien financier.
   

5. Projet USPC « Bifurcations, renormalisation et hyperbolicité non-uniforme », 2015-2018. Porteurs du projet : P. Berger et H. Eliasson.

Flots d’Anosov en dimension 3. Un flots est dit d’Anosov si la variété qui le porte est un ensemble hyperbolique pour ce flot. Ce sont donc, d’un certain point de vue, les flots hyperboliques (voir ci-dessus) les plus simples. Ce sont aussi, d’un autre point de vue,  les flots les plus chaotiques. S’il est relativement facile de donner de tout présentations combinatoires de tout flot d’Anosov, on est cependant bien loin d’une classification, même sur les variétés de dimension 3. Les exemples les plus simples en dimension 3 sont  les suspension d’automorphismes d’Anosov linéaires du tore T^2, et les flots géodésiques sur les fibrés unitaires tangents des surfaces à courbure négative. Des résultats de J. Plante et E. Ghys montrent que certaines variétés ne porte qu’un seul flot d’Anosov, qui est automatiquement l’un des deux exemples cité précédemment. Mais il existe aussi des exemples des flots d’Anosov exotiques. Avec C. Bonatti et B. Yu, nous avons mis au point un procédé de construction de flot d’Anosov par « recollement de morceaux ». Ce procédé permet de fabriquer de nombreux exemples nouveaux de flots d’Anosov pathologiques. Par exemple, nous montrons que, pour tout entier n, il existe une variété de dimension 3 qui porte au moins 3 flots d’Anosov distincts. D’autre part, nous avons décrit un moyen de découper un flot d’Anosov en morceaux élémentaires, et analysé dans quel mesure cette méthode de découpage est canonique. Malgré ces petits progrès, les flots d’Anosov en dimension 3 restent bien mystérieux... 

Ensembles de points fixes non-enlacés. Si f est un homéomorphisme de surface, il est souvent utile de trouver un ensemble F de points fixes de f, le plus gros possible, et tel qu’il existe un chemin continu (f_t) d’homéomorphismes joignant l’identité à f tel que F est contenu dans les points fixes de f_t pour tout t. On dit alors que F est un ensemble de points fixes maximal non-enlacé. Avec S. Crovisier et F. Le Roux, nous montrons l’existence de tels ensembles. Un corollaire simple de ce résultat est que, si f est un homéomorphisme du plan préservant l’orientation, et F un ensemble de points fixes de f, alors il existe un chemin continu (f_t) d’homéomorphismes joignant l’identité à f, tel que F est contenu dans les points fixes de f_t pour tout t.