 |
OptFEM2DP1 Toolbox
V1.2b3
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 2D
|
 |
OptFEM2DP1 Toolbox
V1.2b3
Matlab/Octave Optimized P1-Lagrange Finite Element Method in 2D
|
Validation function for the Assembly of the Stiffness Elasticity Matrix for 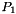 -Lagrange finite elements.
More...
-Lagrange finite elements.
More...
Go to the source code of this file.
Functions | |
| function | validStiffElasP1 (Num) |
Validation function for the Assembly of the Stiffness Elasticity Matrix for 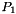 -Lagrange finite elements. -Lagrange finite elements. | |
| function | validStiffElasP1>checkTest1 (Test) |
| function | validStiffElasP1>checkTest2 (Test) |
| function | validStiffElasP1>checkTest3 (h, error) |
Validation function for the Assembly of the Stiffness Elasticity Matrix for 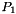 -Lagrange finite elements.
-Lagrange finite elements.
Definition in file validStiffElasP1.m.
| function validStiffElasP1>checkTest1 | ( | Test | ) |
Definition at line 190 of file validStiffElasP1.m.
| function validStiffElasP1>checkTest2 | ( | Test | ) |
Definition at line 205 of file validStiffElasP1.m.
| function validStiffElasP1>checkTest3 | ( | h, | |
| error | |||
| ) |
Definition at line 228 of file validStiffElasP1.m.
| function validStiffElasP1 | ( | Num | ) |
Validation function for the Assembly of the Stiffness Elasticity Matrix for 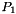 -Lagrange finite elements.
-Lagrange finite elements.
The Stiffness Elasticity Matrix is given by
![\[\StiffElas_{m,l}=\int_{\DOMH} \Odv^t(\BasisFuncTwoD_m) \Ocv(\BasisFuncTwoD_l)dT, \ \forall (m,l)\in\ENS{1}{2\,\nq}^2,\]](form_60.png)
where 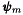 are
are 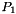 -Lagrange vector basis functions. Here
-Lagrange vector basis functions. Here 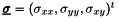 and
and 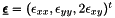 are the elastic stress and strain tensors respectively.
are the elastic stress and strain tensors respectively.
This Matrix is computed by functions StiffElasAssemblingP1{Version} where {Version} is one of base, OptV0, OptV1 and OptV2.
![\[\int_\DOM \Odv^t(\vecb{u}) \Ocv(\vecb{v})d\q \approx \DOT{\StiffElas \vecb{U}}{\vecb{V}}\]](form_81.png)
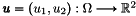 and
and 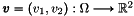 . We have
. We have 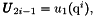
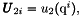

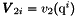 if Num in {0,2} and
if Num in {0,2} and 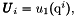
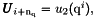
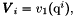
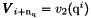 if Num in {1,3}. Use functions
if Num in {1,3}. Use functions 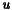 and
and 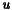 defined in valid_StiffElas.
defined in valid_StiffElas.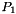 -Lagrange integration
-Lagrange integration
![\[|\int_\DOM \Odv^t(\vecb{u}) \Ocv(\vecb{v})d\q - \DOT{\StiffElas \vecb{U}}{\vecb{V}}| \leq C h^2\]](form_93.png)
Definition at line 17 of file validStiffElasP1.m.